UNIT 19 READING A

Drawing ray diagrams

Even though there are many rays of light from an object that pass through a lens, it is sufficient to draw only two of those rays to find the location of the object. There are three common rays to use. They are given below for a converging lens and a diverging lens.

Converging lens

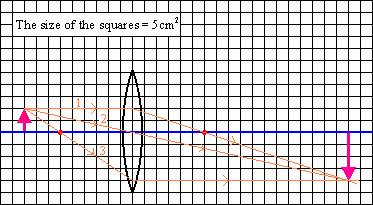
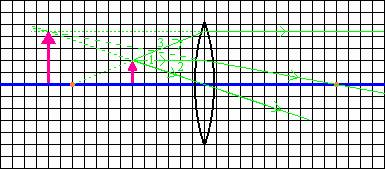
1. A ray from the top of the object that enters the lens parallel to the axis of the lens passes through the focal point on the other side of the lens

2. A ray from the top of the object that passes through the center of the lens leaves the lens at the same angle it enters the lens.

3. A ray from the top of the object through the focal point, would leave parallel to the axis of the lens.

If the object is inside the focal point, the third ray is drawn as if it came from the focal point on the left side of the lens and passes through the top of the object, leaving parallel to the axis of the lens.

The top of the image is located at the point the rays meet.

These are shown in the two diagrams below:

1) for an object located outside the focal point of the lens

and 2) for an object located inside of the focal point of the lens.

Diverging lens

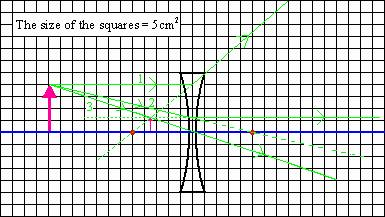
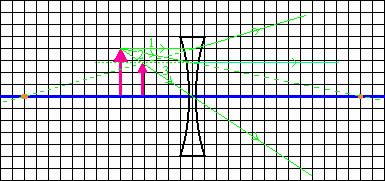
1. A ray from the top of the object that enters the lens parallel to the axis of the lens emerges such that it appears to have passed through the focal point on the front side of the lens

2. A ray from the top of the object drawn toward the focal point on the backside of the lens emerges parallel to the axis of the lens.

3. A ray from the top of the object that passes through the center of the lens leaves the lens at the same angle it enters the lens.

The top of the image is located at the point from which the rays appear to emerge.

These are shown in the two diagrams below:

1) for an object located outside the focal point of the lens

and 2) for an object located inside of the focal point of the lens.

From the diagram, we could measure the distance of the image from the lens. This is called the image distance.

The magnification is the ratio of the image height () to the object height (). It is common to define the magnification to be positive when the image is upright and negative when the image is inverted. If the image is inverted then is considered to be negative.

From geometry, the ratio of the object height to the image height is

It can also be shown (and will not be shown here) that for a thin lens the focal length (), object distance () and image distance () are related by the following equation

with the following set of rules:

1. is positive if the object is to the left of the lens and negative if it is to the right of the lens.

2. is positive if the image is to the right of the lens and negative if it is to the left of the lens.

3. The focal length, , is positive for a convex (converging) lens and negative for a concave (diverging) lens.

The magnification is then defined as

The formula is called the thin lens equation.