UNIT 18
RADIOACTIVITY
Objectives
- to be able to use knowledge of electric and magnetic fields to explore the nature of radiation
- to understand that radioactivity is a statistical process; each unstable nucleus has a probability to decay, but the probability is different for different radioactive materials
- to understand the number of particles emitted from a radioactive sample decreases with time in a predictable way
- to understand the concept of decay rate
- to understand the concept of half-life
Equipment:
3 Radiation sources (Alpha, Beta, and Gamma)
Radiation Monitor
LabPro Computer Interface
LoggerPro software
Excel software
Materials to place between radiation source and radiation monitor
1.1
a. Based on previous knowledge (from other courses or things you have heard or read), how would you answer the question, what is “radioactivity”?
Obtain a Radiation Monitor and radiation source. Place the detector near one of the sources. Move the switch to Audio. You should hear the detector “click” when it is near a source. You will hear a different number of “clicks” per unit time at different distances and at different angles from each of the sources.
b. Based only on the fact that you hear “clicks” when the detector is near the source, what is interesting that you might want to explore about the sources, about the detector? If you knew nothing about matter or the sources, except what you have observed so far, what would you hypothesize about the sources, about the detector?
Connect the detector to the Labpro computer interface with this file. You can set the computer to record the number of “clicks” in a given time interval. In Setup select Data Collection, select Mode and choose Radiation Counting. Then go to Sampling to choose the length of your experiment and the count interval. Go into View select Graph Features unselect Connecting Line and select Bar Graph. To take data, turn the Radiation Monitor on and click on Collect.
c. Put the detector at different distances from the sources and at different angles. Record the number of counts in a 30 sec. or 1 min. interval at different distances and at different angles (at the same distance).
d. Put different materials between the source and the detector. Try different materials of different thickness for each of the three sources. What do you observe?
e. Take more rigorous data. Fix the distance so that you get about twenty counts in a given amount of time (You may choose the time interval.). Take data at that same distance and for the same interval twenty times. Do you get the same number of counts each time? Plot the number of counts per interval on the computer. Determine the average number of counts per interval.
f. Keep the distance from the source the same as in part e, but put different pieces of material between the source and the detector. Take data at that same distance and for the same interval twenty times. How do these data compare to the data in part e?
g. Develop a hypothesis for what is happening, based only on your observations so far.
h. What do you think would happen to the number of counts per interval, if your hand or another part of your body were between the source and the detector? Should you worry about that? Explain.
i. Do you think that the number of counts per interval changes with time? Explain your reasoning.
Equipment:
None
2.1 In Exercise 17 you analyzed the velocity selector shown below. It consists of two capacitor plates with positive charges on the bottom plate and negative charges on the top plate. There is an electric field pointing upwards and a magnetic field pointing out of the page everywhere in between the plates.
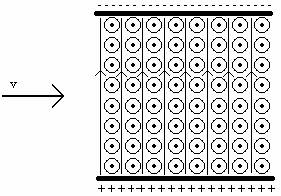
a. Could the velocity detector be used to determine the velocity of whatever is coming out of the radioactive sources? Explain.
b. Could you determine the sign of the charge (positive or negative) of whatever is coming out of the radioactive sources? Explain.
c. Suppose a positively charged particle left the radioactive source, went through the velocity selector and then entered a region of constant magnetic field into the page as shown in the picture below.
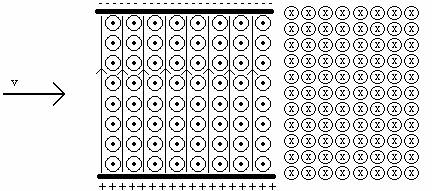
What would be the path of the particle in the region in the constant magnetic into the page? Explain.
d. Write an equation for the ratio of the charge and the mass of the particle in terms of the radius of the path of the particle, magnetic field, and the velocity of the particle.
e. A particle leaving a radioactive source enters a velocity selector and leaves with a velocity v = 2.1 x 106 m/s. It enters a region of constant magnetic field B = 4.38T out of the page and curves to the right with radius r = 0.01m. What is the ratio of the charge to the mass of the particle? Explain.
f. Could the set up in part c be used to analyze whatever is coming out of the radioactive sources? Explain.
Discuss with an instructor.
Three distinct types of nuclear radiation have been identified. They were originally called alpha, beta and gamma rays. Later research, using equipment of the type described in part c., found that the radiation labeled alpha rays were positively charged particles and that the charge-to-mass ratio was that of a Helium nucleus, also called an alpha particle. The radiation labeled beta rays were found to be negatively charged particles with the charge-to-mass ratio of an electron. The radiation labeled gamma rays were found to be electromagnetic waves.
Equipment:
300 dice
3.1
Radioactivity is now understood as a phenomenon in which neutrons and protons in a nucleus transform themselves spontaneously to a more energetically favorable energy configuration (lower potential energy) by emitting a particle. Typically, the particle is a gamma ray, a beta particle, or an alpha particle. After the radiation is emitted, the neutrons and protons that are attracted to each other by the strong nuclear force move closer together.
Radioactivity is a statistical process. Each undecayed nucleus is in an unstable state and could emit a particle at any time. Each unstable nucleus has a probability to decay, but the probability is different for different radioactive samples (different materials). The number of particles emitted from a radioactive sample decreases with time in a predictable way. We are going to model this by considering the behavior of a large collection of dice.
a. Obtain 300 dice. A single die will represent a radioactive nucleus that could decay in a given time period. Every time the dice are rolled represents a time period. For each die there is a probability of 1 in 6 to get a particular number (for example a “4”). So every die that lands with a particular number, say “4”, represents a nucleus that has decayed. We are going to record the number of dice that do not decay every time period.
We start with 300 undecayed dice at time t = 0.
1) Roll all 300 dice at once. This represents the next time period t = 1.
2) Count the number of decayed dice and the number of undecayed dice and record these
numbers in the table below.
3) Remove all the decayed dice.
4) Roll the remaining undecayed dice. This represents time period t = 2.
5) Count the number of decayed dice and the number of undecayed dice and record these
numbers in the table below.
6) Remove all the decayed dice.
7) Repeat the process for 15 time periods.
|
Time |
Number of
undecayed dice |
Number of
decayed dice |
|
0 |
300 |
0 |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
b. Using Excel graph the number of undecayed dice vs. time. Fit the curve to an exponential of the form
![]()
where N(t) is the number of undecayed dice at time t, N(0)
is the number of undecayed dice at time 0 and ![]() (lamda) is the decay constant.
(lamda) is the decay constant.
What is the decay constant of your dice?
c. What is the amount of time that it takes for half the dice to decay?
The time it takes for half of the nuclei in a radioactive
sample to decay is called the half-life of the material. The symbol for
half-life is ![]() (tau) and the units
are seconds.
(tau) and the units
are seconds.
How is the half-life mathematically related to the decay constant? Show your work.
Discuss with an instructor.
d. Suppose the dice decay constant were doubled so the probability of decay in each minute was twice as great. (This could be simulated by claiming that upon each roll of the dice, the decay occurs whenever a “2” or a “6” comes up.) What would happen to the half-life of a collection of dice rolled once a minute?
SUMMARY
You should be able to use knowledge of electric and magnetic fields to explore the nature of radiation. You should understand that radioactivity is a statistical process, that each unstable nucleus has a probability to decay, but the probability is different for different radioactive materials. You should understand the number of particles emitted from a radioactive sample decreases with time in a predictable way and the concept of decay rate. You should understand the concept of half-life