UNIT 12

DIRECT CURRENT CIRCUITS: CAPACITORS

Objectives

· to understand how capacitors behave as elements in circuits

· to understand the definition of capacitance

· to understand how capacitors behave in series and parallel networks and be able to calculate the capacitance of series and parallel networks

Equipment:

1 voltmeter

2 wires with alligator clips

1 battery

1 battery holder

1 capacitor

1.1 Consider a capacitor connected to a battery as in the diagram below.

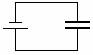
a. Discuss in terms of charges and electric fields what happens. If current flows, describe why. Is the current constant with time? Is it zero? Does it change? Is it the same in different parts of the wire?

b. If after a long time the capacitor were disconnected from the battery, would there be a net charge on the capacitor?

c. Would there be a reading on the voltmeter, if you attached a voltmeter across the capacitor? Explain.

d. If, after the capacitor has been disconnected from the battery, you connected one end of the capacitor to a large piece of metal, what if anything would happen? Explain.

e. If, after the capacitor has been disconnected from the battery, and you connected one end of the capacitor to a large piece of metal, as in part d, would there be a reading on a voltmeter, if you attached a voltmeter across the capacitor? Explain.

f. Connect the battery to the capacitor as in the diagram above. After the capacitor has been connected for two minutes, disconnect the battery from the capacitor. Carry out the experiments described in parts c, d, and e above. Explain.

Equipment:

None

2.1

a. Is the potential difference across the plates of a capacitor related to the amount of charge on the plates? Explain.

b. The constant of proportionality between the amount of charge on one of the plates and the potential difference between the plates is called the capacitance:

The symbol for capacitance is C. The unit of capacitance is Farad (F). One Farad is equal to one Coulomb per Volt, 1F = 1C/V.

Equipment:

3 ammeter

8 wires with alligator clips

1 bulb

1 socket

1 battery

1 battery holder

1 switch

2 capacitor

1 nichrome wire

3.1 Consider the following circuit.

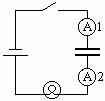
a. Qualitatively, what would the ammeters read as a function of time after the switch was closed? Describe whether they would increase, decrease or remain the same. Would ammeter 1 read the same as ammeter 2 sometimes? All the time? Explain.

b. Set up the circuit and test your prediction. Explain the readings on the ammeters in terms of charges and electric fields.

3.2 Consider the following circuit.

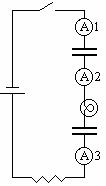
a. Qualitatively, what would the ammeters read as a function of time after the switch was closed? Describe whether they would increase, decrease or remain the same. Would ammeters 1, 2 and 3 read the same all the time? Sometimes? Explain your reasoning.

b. Set up the circuit and test your prediction. Explain the readings on the ammeters in terms of charges and electric fields.

Equipment:

None

4.1 Consider two capacitors of different capacitances connected in parallel across a battery as shown below.

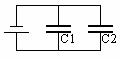
a. Is the potential difference between the plates of each capacitor the same? Explain. Do the two capacitors have the same amount of charge on each of their plates? Explain.

b. How are the two capacitors like a single capacitor? Could you replace the two capacitors with a single capacitor? If so, what would be the charge, Q, on that capacitor in terms of the charges (Q₁ and Q₂) on the original capacitors? Write this in terms of an equation.

Use the equation that relates the charge Q on the new capacitor to the charges Q₁ and Q₂ and the relationship between charge and potential difference for each capacitor to find the capacitance of the replacement capacitor in terms of the capacitances C₁ and C₂ of the original two capacitors.

Discuss your relationship with an instructor.

4.2 Consider two capacitors of different capacitances connected in series across a battery as shown below.

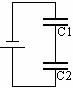
a. Do the two capacitors have the same amount of charge on each of their plates? Explain. Is the potential difference between the plates of each capacitor the same? Explain.

b. How are the two capacitors like a single capacitor? Could you replace the two capacitors with a single capacitor? If so, what would be the potential difference, DV, across the replacement capacitor in terms of the potential differences across each of the original capacitors? Write this in terms of an equation.

Use the equation that relates the potential difference DV on the new capacitor to the potential differences DV₁ and DV₂ and the relationship between charge and potential difference for each capacitor to find the capacitance of the replacement capacitor in terms of the capacitances C₁ and C₂ of the original two capacitors.

Discuss your relationship with an instructor.

Equipment:

None

3.1 A defibrillator is a large capacitor.

When a defibrillator is discharged across a body, the current through the heart is about 6 amps. Compare this to the currents on the chart in the handout on the effect of different amounts of current on the human body. Explain.

SUMMARY

You should understand how capacitors behave as elements in circuits. You should understand the definition of capacitance. You should understand how capacitors behave in series and parallel networks and be able to calculate the capacitance of series and parallel networks.