UNit 5
electrical potential
difference
Objectives
- to understand the concept of electric potential energy
- to understand the concept of electric potential difference as the work per unit charge done by an agent in moving a charge from one point to another
1.1 Let’s review some old definitions in preparation for tackling the idea of work and energy expended in moving through an electric field. Work is defined mathematically as the component of force in the direction of motion of an object times the magnitude of the displacement of the object
![]()
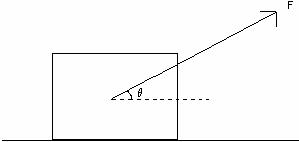
For example, if a
box is moving in the horizontal direction across the floor, as in the picture
below, the work done by the force F is ![]() times the magnitude of the displacement traveled, d, across the floor.
times the magnitude of the displacement traveled, d, across the floor.
If the object moves from an initial to a final point by moving along a series of paths in different directions, the net work is the sum of the work over each of the individual paths.
The gravitational force is a conservative force. Work done by a conservative force is independent of path. Therefore, work done by the gravitational force is independent of path. If a force is a conservative force, the work done by that force can be written as the negative of a change in potential energy. The work done by the gravitational force can then be written as
![]()
The work done by the electric force when an object is moved from point a to point b in a constant electric field is
![]()
where ![]() is the magnitude of
the electric field,
is the magnitude of
the electric field, ![]() is the charge,
is the charge, ![]() is the final position,
is the final position,
![]() is the initial position and
is the initial position and ![]() is the angle between
the electric field and the direction of motion. Since the electric field, like
the gravitational field is a conservative field, the work depends only on the
endpoints.
is the angle between
the electric field and the direction of motion. Since the electric field, like
the gravitational field is a conservative field, the work depends only on the
endpoints.
The existing experimental evidence is that the electric force is a conservative force. Since it is a conservative force, we can define a potential energy such that
![]()
The electric potential energy is
![]()
a.
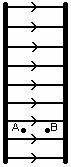
Consider the diagram below.
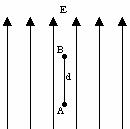
(i) If a positive charge q travels a distance d from point A to point B, as in the diagram above, along a path parallel to a uniform electric
field of magnitude E is the work done by the field on the
charge positive, negative or zero? Explain your reasoning. How does the form of this equation compare to
the work done on a mass m traveling a
distance d in the almost uniform
gravitational field near the surface of the earth?
(ii) If the charge were negative, would the work done by the field be positive, negative, or zero? Explain your reasoning.
(iii) If you were to calculate the work divided by the charge in parts (i) and (ii) above, would that quantity (work done by the electric field divided by the charge on with the work is done) be positive, negative, or zero?
The negative of the work done by the electric force in moving a charge from an initial point to a final point divided by the charge (-Welec/q) is called the change in electrical potential or the voltage. The symbol for electrical potential is V and the change in potential is written as
![]()
(iv) In the diagram above, at which point is the potential highest, point A or point B?
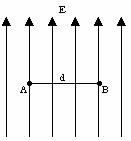
b. Consider the diagram
below.
(i)
The charge +q travels a distance d from point A to point B in a uniform
electric field of magnitude E, but
this time the path is perpendicular to the field lines. What is the work done by the field on the
charge? Explain your reasoning.
(ii) The charge - q travels a distance d from point A to point B in a uniform
electric field of magnitude E, but
this time the path is perpendicular to the field lines. What is the work done by the field on the
charge? Explain your reasoning.
(iii) What is the potential difference between points A and B in this case?
c.
Consider the diagram below.
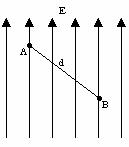
(i) A charge +q travels a distance d
from point A to point B in a uniform electric field of
magnitude E. The path lies at a 45° angle to the field
lines. What is the work done by the field on the charge? Explain your
reasoning.
(ii) A charge - q travels a distance d
from point A to point B in a uniform electric field of
magnitude E. The path lies at a 45° angle to the field
lines. What is the work done by the field on the charge? Explain your
reasoning.
(iii) Is the potential difference between point A and point B positive or negative? Explain your reasoning.
d. Consider the three diagrams below.
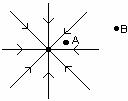
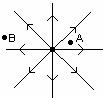
In each diagram determine which point is at a higher
potential, point A or point B.
e. Can you find a simple rule to determine which of two points is at a higher potential?
Share your rule with an instructor.
Equipment:
EKG sensor
EKG electrodes (3 for each person)
LabPro computer interface
Logger Pro software
Excel program
EM Field program
2.1 An electric dipole is two charges of the same magnitude and opposite sign placed relatively close to each other, as in the diagram below.
![]()
a. Consider two points A and B, near the electric dipole, as in the diagram below. It is possible to calculate the potential difference, work per unit charge, between points A and B. We will not do the calculation. We will let EM Field program do it for us.

In the EM Field program set up the grid and place two charges of equal magnitude and opposite sign five units apart. Choose potential difference under field and potential on the tool bar and find the potential difference between two points, for example, A and B in the diagram above. Do this by clicking on one point and dragging the curser to the second point.
(i) If you were to move the charges closer together, would the potential difference between the points change? Explain your reasoning.
(ii) Move the charges closer together in the EM Field program, and test your prediction.
(iii) Move the charges around to different locations on the screen in EM Field program and observe the change potential difference between the two points.
b. Your heart is like an electric dipole with the charges constantly moving around. Actually it is more complicated, but we will model it like an electric dipole. You can measure the potential difference between two points on your body due to the change in position of the charges in your heart. This is called an electrocardiogram (EKG or ECG).
Obtain an EKG sensor, EKG electrodes, and a LabPro computer interface. Open the File EKG sensor. You may also want to use the EKG strip chart selection. Follow the direction on page 5 of the EKG instructions for connecting the EKG sensors to a person. Record the EKG for each person in your group. Save your EKG to a file, so you can print it out.
c. Go back the EM Field program and set up the electric dipole as in part a. Then try to move the charges in such a way as to reproduce your EKG reading, by recording and plotting in Excel, the difference of potential between two points.
d. You may want to read the details of how the heart works in the EKG sensor instructions.
Discuss your results with an instructor.
SUMMARY
You should understand the concept of electric potential
energy. You should understand the concept of electric potential difference as
the work per unit charge done by an agent in moving a charge from one point to
another.