UNIT 3
ELECTRIC FIELD
Objectives
- to understand the concept of an electric field qualitatively and quantitatively
- to be able to represent the electric field at a point in space by a vector
- to understand the principle of superposition as applied to electric fields
- to understand how to represent an electric field with field lines
- to understand that the electric field at the surface of a conductor in static
equilibrium is perpendicular to the surface
- to understand that the electric field is zero inside a conductor in static equilibrium
- to understand how a Faraday Cage works in terms of electric fields and charges
Equipment:
None
1.1 Suppose you had an object that had a positive charge of 100C.
a. If there were an object with 5C of charge 5m away from the 100C object, what would be the magnitude of the force that object would experience? What value do you get, if you divide the magnitude of the force the object experiences by the charge of the object?
b. If there were an object with 15C of charge 5m away from the 100C object, what would be the magnitude of the force that object would experience? What value do you get, if you divide the magnitude of the force the object experiences by the charge of the object?
c. If there were an object with 1C of charge 5m away from the 100C object, what would be the magnitude of the force that object would experience? What value do you get, if you divide the magnitude of the force the object experiences by the charge of the object?
d. If there were an object with 20C of charge 10m away from the 100C object, what would be the magnitude of the force that object would experience? What value do you get, if you divide the magnitude of the force the object experiences by the charge of the object?
e. If there were an object with 4C of charge 10m away from the 100C object, what would be the magnitude of the force that object would experience? What value do you get, if you divide the magnitude of the force the object experiences by the charge of the object?
f. If there were an object with 1C of charge 10m away from the 100C object, what would be the magnitude of the force that object would experience? What value do you get, if you divide the magnitude of the force the object experiences by the charge of the object?
g. Record your results from parts a through f in a table. In each case, include the charge of the object, the distance of the object from the 100C object, the magnitude of the force on the object and the magnitude of the force on the object divided by the magnitude of the charge of the object.
h. Add the results for an object with 10C of charge at 15m from the 100C object. Predict the results for the magnitude of the force on the object divided by the magnitude of the charge of the object for a 2C charge at the same distance.
i. What observations can you make about the magnitude of the force on the object divided by the magnitude of the charge of the object?
Equipment:
1 rubber rod
1 piece of fur
1 metal-coated pith ball hung from non-conducting threads
1 glass rod
2 stands for rubber rods
1 piece of silk
2.1 The electric field is a vector quantity defined at a point in space as the force that would be experienced by a small positively charged object placed at that point divided by the charge of the object:
![]()
q is a small
positive charge. If a small positively charged particle is located at a point
in space, the electric field at that point in space is the force on that
particle divided by the charge. If there is no charge at a point in space, the
electric field at that point can be determined by placing a small positive test
charge at that point and finding the force on that charge in order to determine
the electric field at that point in space.
The units of electric field are N/C.
a. To investigate the vector nature of an electric field, use a negatively charged, metal-coated ball, suspended from a string, as the test charge. ( The ball is charged by touching it with a rubber rod that has been rubbed with rabbit fur.) Charge up the rubber rod by rubbing it with rabbit fur and place it in an insulating stand in a vertical position. Now hold the test charge by its string and move it around the rod. Note the direction and magnitude of the force at various locations around the rod.
Make a qualitative sketch of some of the electric field vectors around the rod at the points in space marked on the following diagram. The length of each vector should roughly indicate the relative magnitude of the field (that is, if the E-field is stronger at one point than another, make its vector longer). Of course, the direction of the vector should indicate the direction of the field. Put the tail of the vector at the location of interest.
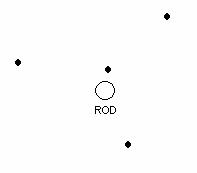
b. How would the diagram change if the negatively charged rod were replaced with a positively charged rod? Draw the new diagram below.
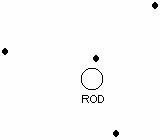
Check with an instructor.
2.2
a. Suppose you had two charged rods, one charged positively and one charged negatively, about 3cm apart. Predict the relative magnitude and the direction of the electric field at each point indicated in the diagram below. Explain your reasoning for your predictions.
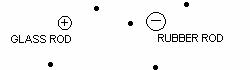
b. Check your predictions in part a by performing the experiment.
The principle of superposition states
that the electric field at a point in space can be found by the vector addition
of the electric fields at that point in space due to all charged objects.
c. Is this consistent
with your answers to part a and part b above?
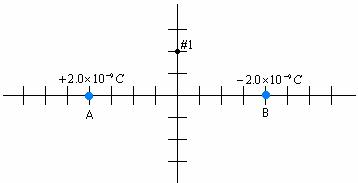
d. The following graph shows
two point particles with charges of +2.0 ´ 10–9 C
and –2.0 ´
10–9 C that are separated by a distance of 8.0 cm. They are fixed so
that they cannot move.
(i) Calculate the value of
the electric field at point 1 due to charge A.
(ii) Calculate the value of the electric field at point 1 due to charge
B.
(iii) Use the principle of superposition to calculate the total electric field at point 1.
Equipment:
1 EM Field Program
3.1
You have been representing the electric field due to a configuration of electric charges by an arrow that indicates magnitude and direction. This is the conventional representation of an electric field. An alternative representation of the vector field involves defining electric field lines.
Below is a series of diagrams with electric field lines drawn for +1C, +2C, and -1C charges.
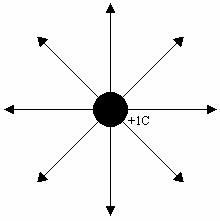
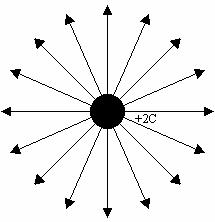
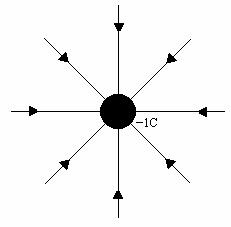
a. From looking at
the diagrams how do you tell where the field is strongest? Explain. How do you tell where the field is weakest?
How do you tell the direction of the field? Explain.
b. Based on the diagrams for electric field lines, draw a diagram with electric field lines for +3C charge.
c. Draw an electric field line diagram for –4C charge.
d. Is there an electric field at points in space where there are no electric field lines drawn? Explain.
Below is the electric field line diagram for two charges, +2C and –2C.
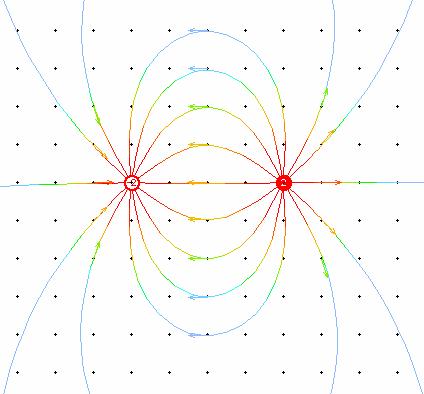
(Drawn in EM Field by D. Trowbridge and B. Sherwood, Physics Academic Software, 1998)
Below is the electric field line diagram for two charges, -1C and +2C.
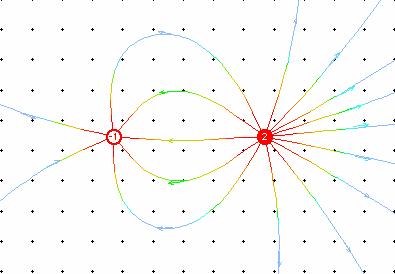
(Drawn in EM Field by D. Trowbridge and B. Sherwood, Physics Academic Software, 1998)
e. Draw an electric field line diagram for a -2C and -2C point charge in the space below.
f. Determine a set of rules for drawing electric field lines for charges. Explain how your rule generates a diagram that contains information about the magnitude and direction of the electric field.
Discuss your rule with an instructor.
3.2
a. Open the EM Field program and use it to draw field
lines for different configurations of charges. Are the field lines consistent
with your rules for drawing field lines? Are they different from the
field lines you would have drawn? Explain.
Equipment:
1 Wimshurst machine
2 large metal plates
1 metal-coated pith ball
2 wires with alligator clips
4.1 A Wimshurst machine is a machine that can be used to charge objects positively or negatively.
a. When a Wimshurst machine is connected to two large plates of metal , one of the plates is charged positively, and one of the plates is charged negatively. Draw the charge distribution for two large metal plates, one charged positively and one charged negatively, in the diagram below.

Now draw the electric field lines in the above diagram.
Discuss your sketch with an instructor.
b. Based on the field lines you drew, how does the magnitude of the field outside the plates compare magnitude of the field inside the plates? Explain.
c. How does the magnitude of the field at different points between the plates compare? How does the magnitude of the field at point A compare to the magnitude of the field at points B, C, and D in the diagram below?
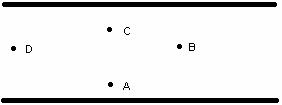
d. Obtain a Wimshurst machine, two large metal plates and a metal coated pith ball. Attach the Wimshurst machine to two metal plates mounted horizontally. Put the pith ball on the bottom plate and turn the crank. The plates will become charged, one positively and one negatively. We will discuss how the Wimshurst machine works at a later time. Consider only the plates and the pith ball. Explain what happens and why.
The configuration of two charged conductors, one charged positively and one charged negatively, is called a capacitor. When the two charged conductors are parallel plates of metal, we call it a parallel plate capacitor. We will talk about capacitors again at a later time.
Equipment:
1 styrofoam cup
Aluminum foil
Pencil
String
1 Paperclip
1 rubber rod
1 piece of fur
1 Faraday’s cage
1 Van de Graaff generator
5.1
a. Suppose you put a piece of metal near a charged object as in the diagram below. Approximately how would the charges arrange themselves in the metal? Draw the charges in the diagram.

b. As the charges arrange themselves, while they are
still moving, does the electric field inside the metal due to the external
charged object change? Is there
an electric field inside the metal due to other charges, besides the external
charged object? As the charges arrange themselves, while they are still
moving, does the total electric field inside the metal change? Explain your reasoning.
c. If all of the charges have stopped moving, is there an electric field inside the metal? Explain. Is there an electric field at the surface of the metal?
Discuss your reasoning with an instructor.
When there are no moving charges inside a metal, the metal is said to be in static equilibrium.
d. Is there an electric field inside a conductor in static equilibrium? Explain.
e. If there was electric field at an angle away from the surface of a piece of metal, as in the picture below, would there be an electric field parallel to the surface of the metal? Would there be an electric field perpendicular to the surface of the metal? If there were an electric field parallel to the surface of the metal, would charges inside the metal move due to that component of the field? If there were an electric field perpendicular to the surface of the metal, would charges inside the metal move, due that component of the field? Explain.
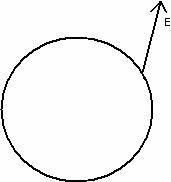
.
f. If a piece of metal is in static equilibrium, what direction is the electric field at the surface of the metal?
Discuss your answers to parts e and f with an instructor.
g. Consider a piece of metal near a charged object, as in part a above. If, after a period of time, the object is in static equilibrium (all of the charges in the metal have stopped moving), you drill a hole in the metal, how would the charges arrange themselves? Draw a picture of the new charge arrangement.
h. Consider the set-up in part g after drilling the hole. What is the value for the electric field inside the hole? Explain your reasoning.
i. Take a Styrofoam cup and cover it with aluminum foil. Hang a paper clip from a string inside the cup by suspending it from a pencil, laying it across the top of the cup. Predict what would happen to the paperclip if a charged rod were brought near the side of the cup. Test your prediction. Is your observation consistent with parts g and h? Explain.
Check your answer with an instructor.
5.2
A space surrounded by metal is called a Faraday cage.
a. Based on your observations in the previous section and your predictions based on your model for how charges distribute themselves inside a metal in section 5.1, what is the magnitude of the electric field inside a Faraday cage when a charged object is brought near the outside of the cage? Draw a picture and explain your reasoning. Would the magnitude of the electric field in a space not completely surrounded by metal (like the Styrofoam cup covered with foil in part 5.1.i) be the same as in a space completely surrounded by metal?
b. Predict whether or not the magnitude of the electric field inside the Styrofoam cup would change, if you were to start cutting holes in the aluminum around the Styrofoam cup. Would the number of holes you cut and the size of the holes matter? Explain your reasoning.
c. Perform the experiment in part b.
d. Consider the large space enclosed by chicken wire (ask an instructor to show it to you). Predict the magnitude of the electric field inside the space enclosed by the wire when there is a Van de Graaff generator outside. A Van de Graaff generator is a mechanism for putting a lot charge on a metal ball. Figure out a way to test the relative magnitude of the electric field near the Van de Graaff generator and inside the space enclosed by the wire when the Van de Graaff generator is near the wire. Carry out the tests you devised to see if your predictions are correct.
e. Why would a Faraday cage be useful? Explain.
SUMMARY
You should understand the concept of an electric field qualitatively and quantitatively. You should be able to represent the electric field at a point in space by a vector. You should understand the principle of superposition as applied to electric fields. You should be able to represent an electric field with field lines and be able to interpret a field line representation of an electric field. You should understand that the electric field at the surface of a conductor in static equilibrium is perpendicular to the surface and that the electric field is zero inside a conductor in static equilibrium. You should understand how a Faraday Cage works in terms of electric fields and charges.