UNIT 2
COULOMBíS LAW
Objectives
- to understand Coulombís Law qualitatively and quantitatively
- to understand the principle of superposition
Equipment:
1 Electric Field Hockey program
1.1 Open the program Electric Field Hockey and play the Level 1 game.
Equipment:
2 rod stands
1 rubber rod
1 piece of fur
4 metal rods
2 right angle clamps
††††† 2 metal-coated pith ball hung from non-conducting threads
††††† 2 rod hooks
2.1 Consider two identical conducting spheres. One conductor is touched with a rubber rod that has been rubbed with fur. The sphere that has been touched with the rod is now charged. Letís say that it has a negative charge q.
Draw a picture of how the excess charge q is distributed on the sphere. Remember that a sphere with charge q has both positive and negative charges, but more negative than positive charges. The symbol q represents the additional negative charges, the excess negative charge. It is common only to draw the additional charges, with the understanding that the object contains positive and negative charges, but more negative charges. Explain how the charges would be distributed on the sphere.
If the two spheres were now touched together, how would the charge be distributed? How much charge would be on each sphere?† Explain your reasoning.
2.2 Consider a pair of conductors hanging from non-conducting strings, as in the diagram below. Each of the conductors has a charge q.
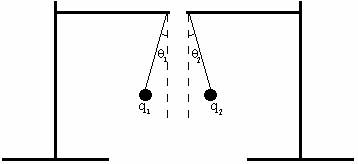
Initially the conductors are placed a certain distance apart. Make predictions for the following situations:
a. Initially, how does the angle with respect to the vertical for charge q1 compare with the angle with respect to the vertical for charge q2? Explain your reasoning.
b. If the conductors are moved closer together, would the angle with respect to the vertical for each conductor increase, decrease or remain the same?† How does the angle with respect to the vertical for charge q1 compare with the angle with respect to the vertical for charge q2? Explain your reasoning.
c. If the conductors are moved farther apart, would the angle with respect to the vertical for each conductor increase, decrease or remain the same? How does the angle with respect to the vertical for charge q1 compare with the angle with respect to the vertical for charge q2? Explain your reasoning.
d. If the conductors were moved back to their initial position and the amount of charge of each conductor was decreased to q/2, would the angle with respect to the vertical for each conductor increase, decrease or remain the same? How does the angle with respect to the vertical for charge q1 compare with the angle with respect to the vertical for charge q2? Explain your reasoning.
e. If the conductors were moved back to their initial position and the amount of charge on conductor q1 was decreased to q/2 (the other conductor, q2, still has charge q), would the angle with respect to the vertical for each conductor increase, decrease or remain the same? How does the angle with respect to the vertical for charge q1 compare with the angle with respect to the vertical for charge q2? Explain your reasoning.
f. Carry out each of the above experiments in parts a
Ė e above and record your observations.
Equipment:
††††††††††† None†††
3.1 Draw force diagrams for the two conductors for
each of the cases below. For each force indicate the type of force (normal,
gravitational,Ö), the object exerting the force and if the force is a contact
force or non-contact force. Indicate all the
a. Neither of the conductors is charged.
b. Both of the conductors have the same amount of charge.
c. One of the conductors has half the amount of charge as the other conductor.
Check your answers with an instructor.†
3.2 Based on your observations, how would you answer the following questions?
a. How does the force of one charged object on another depend on the charge of each of the objects?
b. How does the force of one charged object on another depend on the distance between the two objects?
c. How would you record your answers to a and b above in the form of an equation?
Equipment:
††††††††††† None
4.1 Coulombís Law states that the force of charged object One on charged object Two, F12, equal to the force of charged object Two on charged object One, F21,† (this is Newtonís Third Law), the magnitude of the force is given by
![]() ,
,
and the direction of the force is along a line between the two objects. In the equation, Q1 is the charge of object 1, and Q2 is the charge of object 2, and r is the distance between the objects. Charge is measured in Coulombs represented by the symbol C.† The k in the equation is a constant and has the value 9.0 ī 109 Nm2 /C2. It applies to the force between two small charged objects, so small that all the charge can be considered to be at one point. These are often called point charges.
a. If the sign of† both charges is positive,
∑ which direction is the force of object Two on object One?
∑ which direction is the force of object One on object Two?
∑ is the force positive or negative?
b. If the sign of† both charges is negative,
∑ which direction is the force of object Two on object One?
∑ which direction is the force of object One on object Two?
∑ Is the force positive or negative?
c. If the sign of one charge is positive and the sign of the other charge is negative,
∑ which direction is the force of object Two on object One?
∑ which direction is the force of object One on object Two?
∑ is the force positive or negative?
d. What does the sign of the magnitude of the force tell you?
Equipment:
2 rod stands
1 rubber rod
1 piece of fur
3 metal rods
2 right angle clamps
††††† 2 stands for rubber rods
††††† 1 metal-coated pith ball hung from non-conducting threads
††††† 1 rod hook
†††††
5.1 Assume a negatively charged conductor-coated pith ball is hanging near a negatively charged rod, as in the picture below.
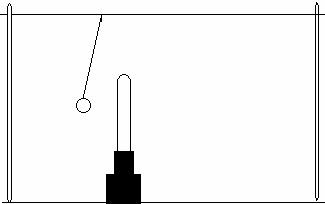
a. If a second negatively charged rod were brought in from the right of the first rod, would the angle of the pith ball change? Explain your reasoning.
b. If a second negatively charged rod were brought in from the left of the pith ball, would the angle of the pith ball change? Explain your reasoning.
c. Carry out the experiment in parts a and b
and record your observations.
d.†† In each of the cases above, does the force on the pith ball depend on both rods?
When more than two point charges are present, the force between any pair of charges is given by Coulombís Law.† Therefore, the resultant force on any one of the charges is the vector sum of the forces due to the other individual charges.† This is called the principle of superposition.
e.† Is this consistent with your observations?
Discuss with an instructor.
Equipment:
1 Electric Field Hockey program
6.1 Play Electric Field Hockey Level 3. Think about strategy based on what you have learned in this section.
SUMMARY
You should understand Coulombís Law qualitatively and quantitatively and be able to work problems using Coulombís Law and you should understand the principle of superposition.