UNIT 16 READING A

Moment of inertia and rotational kinetic energy

Consider an object of mass m moving in a circle about an axis as in the picture below.

The kinetic energy of the object is

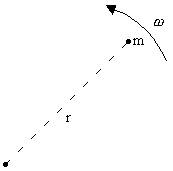
This can be written in terms of the angular speed of the object, , and the distance of the object from the axis of rotation, r

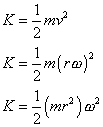
The quantity mr² is defined to be the moment of inertia of the mass m. The kinetic energy can then be rewritten in terms on the moment of inertia

For a large object, we can consider it made up of many smaller pieces of mass.

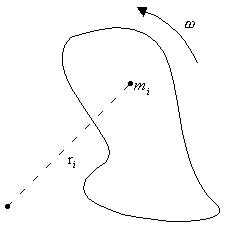
Each piece of mass, m_i, is at a different distance, r_i, from the axis of rotation. The kinetic energy of the object is found by summing up the kinetic energies of each the small pieces of mass:

This can be written as

where is the moment of inertia of the object. This is the rotational kinetic energy of an object.

A rolling object has both rotational and translational kinetic energy, the total kinetic energy for a rolling object is

where I is the moment of inertia of the object, is the angular speed of the object, M is the mass of the object and is the velocity of the center of mass of the object.