UNIT 7
Uniform Circular Motion
(Priscilla
W. Laws, Workshop Physics Activity Guide, John Wiley & Sons, Inc.,
New York, 1999)
The following exercises will take you through a proof that shows that the acceleration of an object traveling in a circle is given by
![]()
a. Refer to the diagram that follows. Explain why, at the two points shown on the circle, the angle between the position vectors at times t1 and t2 is the same as the angle between the velocity vectors at times t1 and t2.
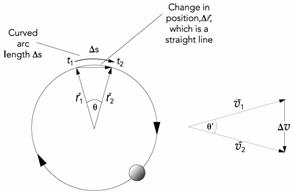
b. Since the angles are the same and since the magnitudes of the positions never change (i.e., r = r1 = r2) and the magnitudes of the velocities never change (i.e., v = v1 = v2), use the properties of similar triangles to explain why
![]()
c. Now use the equation in part b and the definition of average acceleration to show that
![]() .
.
d. The speed of the object as it rotates around the circle is given by
![]()
Is the change in arc length, Ds, larger or smaller than the magnitude of the change in the position vectors, Dr? Explain why the arc length change and the change in the position vector are approximately the same when Dt is very small (so that the angle q becomes very small)—that is, why is Ds » Dr?
e. If Ds » Dr, what is the equation for speed in terms of Dr and Dt?
f. Using the equation in part c, show that as Dt ® 0, the instantaneous value of the centripetal acceleration is given by
![]()
g. If the object has a mass m, what is the equation for the magnitude of the centripetal force needed to keep the object rotating in a circle (in terms of v, r, and m)? In what direction does this force point as the object rotates in its circular orbit?
Law of Gravitation
We have observed that there is a force between Earth and
objects near the surface of Earth – Earth exerts a force on an object and, by
![]()
is the magnitude of the force of one object on the other. M1 is the mass of one object, M2 is the mass of the second object, r is the distance between the center of the two objects, and G is the gravitational constant. G has been determined experimentally to be
6.67 x 10-11 Nm2/kg2.
By
![]()
![]()
where ME is the mass of the earth and Mo is the mass of the object. From this we can solve for the acceleration of an object near the surface of Earth.
![]()
The mass of Earth is 5.98x1024kg and the radius is 6.37x106m.
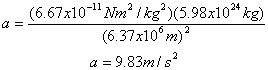
Which is the acceleration we measure near the surface of Earth.