UNIT 6 READING A

Torque

Torque is defined as the product of the distance from the pivot point to the point where the force is applied and the magnitude of the component of the force that is perpendicular to a line through the pivot point and the point of application of the force. If the force causes a clockwise turning, the force is positive; if the force causes a counterclockwise turning, the torque is negative.

We will call r the distance between the pivot point and the point of application of the force F, as in the picture below.

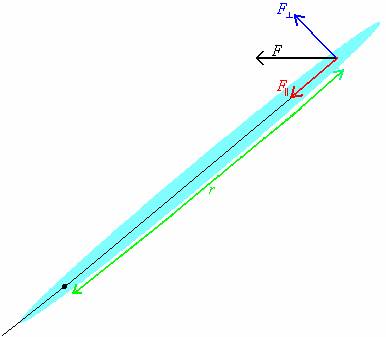
The force can be considered to be the sum of two forces, one parallel to a line through the pivot point and the point of application of the force, F_||, and one perpendicular to a line through the pivot point and the point of application of the force, F_^, as shown in the diagram above. Only the component of the force that is perpendicular to a line through the pivot point and the point of application of the force causes the object to rotate, contributing to the torque. The torque, t, is the quantity r times :

t = r

where r is the distance between the pivot point and the point of application of the force and F_^ is the magnitude of the force. The torque is positive if the force creating it causes a clockwise turning, the force is positive; the torque is positive if the force creating it causes a counterclockwise turning, the torque is negative.

Center of gravity

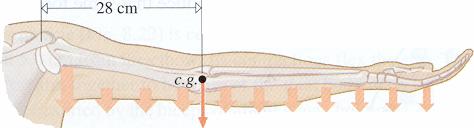
Consider an object free to rotate, as the arm pictured below.

(Eugene Hecht, Physics: Algebra/Trig Second Edition, Brooks/Cole Publishing Company, New York, 1998)

Take the pivot point to be located at the shoulder joint, as in the picture above. The arm can be considered to be made up of many pieces of mass. Each piece of mass produces a torque, the gravitational force acting on the mass times the distance of the mass from the shoulder, about the shoulder joint. The net torque about the shoulder joint is the sum of the torques due to each of the masses.

The same torque could be produced by considering the total weight of the arm to be located at a single point. That point is called center of gravity, as pictured above.

It is possible to calculate the center of gravity of an object. For a symmetric object, the center of gravity is located at the center of the object. In this course, if the object is not symmetric, the location of the object’s center of gravity will be given.

Example Problem:

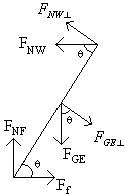
A ladder of length L and mass M is leaning against a wall, as shown in the picture below. The coefficient of static friction between the ladder and the floor is m. The weight of the ladder can be considered to act at its center of mass. Find the minimum angle at which the ladder will not slip.

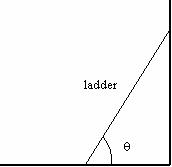
(1) Focus on the Problem: What’s going on?

A ladder is leaning against the wall. At the base of the ladder, there are two forces acting, the normal force of the floor on the ladder and the frictional force. At top of the ladder there is a normal force due to the wall. The gravitational force is acting at the center of the ladder. There are torques due to these forces. If the angle is large enough, the net torque and the net force are zero, and the ladder is in equilibrium. If the angle is too small, then the ladder will no longer be in equilibrium and it will fall.

We want to find the minimum angle at which the ladder is in equilibrium.

(2) Describe the Physics: What is the physics?

Draw a force diagram.

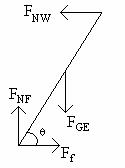
Apply Newton’s second law in both the x- and y- directions. Use the fact that the acceleration is zero in both the x- and y- directions:

Find the net force in each direction.

In the x-direction:

In the y-direction:

where

so

The net torque must be zero. We will take the torque about the point at which the ladder is in contact with the floor. If we make this choice then the torque due to the frictional force and the torque due to the normal force of the floor are zero, because their distance from the pivot point is zero.

Find the components of each of the forces that are perpendicular to a line through the pivot point and the point of application of the force and the net torque.

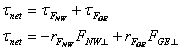
where the negative sign indicates that the torque is in the counterclockwise direction and F_NW^ and F_GE^ are the magnitudes of the perpendicular components of the forces.

So

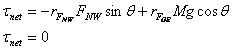
(3) Plan the Solution: Can we find the solution?

From the equations for net force and the relationship between the frictional force and the normal force due to the floor we have the following:

net force and the net torque in each direction is zero and knowing

also

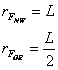
(4) Execute the Plan: What is the answer?

Using the first three equations, we can solve for F_NW in terms of F_GE, which is known.

So

now using the equation for net torque

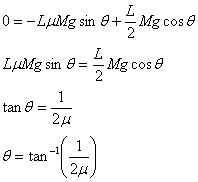
(5) Evaluate the Answer: Can this be true?

The angle is independent of the length and the mass of the ladder.

As the coefficient of friction gets larger, the minimum angle gets smaller, which makes sense.