UNIT 4 READING B
Force Diagrams
You have learned in lab about four different types of forces Ė normal, gravitation, tensile, and frictional. In this class, force diagrams will be drawn as follows:
1) The object on which the forces are acting will be represented by a dot.
2) The forces will be drawn as arrows pointing in the direction of the force, with the tail of the arrow on the dot.
3) Each force should be labeled: for each force, the type of force should be indicated and it should be clear which object is exerting the force.
In our study of kinematics, we found that the equations of motion can be applied independently to the x- and y- directions. Similarly, the x- and y- components of forces are independent of each other. So the equation Fnet = ma, can be written as two equations,
![]() ††††††††††††††††††††††††††††
†††††††††††††††††††††††††††† ![]()
one in the x-direction and one in the y-direction.
For objects at rest, the acceleration is zero. By
Example Problem:
You are helping a friend move into a new apartment. A box weighing 450kg needs to be moved to make room for a couch. You are taller than the box, so you push down at an angle of 50 degrees from the horizontal with a force of 1000N to try to move the box. The box does not move.
(a) What is the frictional force while you are pushing? Show your work.
(b) Your friend tries to move the box with a force of 1100N at an angle of 35 degrees. Your friend cannot move the box either. What is the frictional force while your friend is pushing? Show your work.
(c) The coefficient of static friction between the box and the floor is 0.45. If you and your friend push together, each pushing with the same force and at the same angle as you pushed in parts a and b, can you move the box? Explain your reasoning.
Part (a):
(1) Focus on the Problem: Whatís going on?
You push on a box and it doesnít move. You want to find the frictional force while you are pushing on the box. Since the box is not moving, the acceleration is zero and the net force on the box is zero. You can use the fact that the net force is zero in both the x- and y- directions to find the frictional force.
(2) Describe the Physics: What is the physics?
Draw a force diagram for the box.
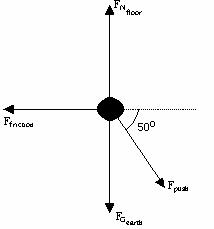
Choose the x-axis to be parallel to the frictional force and
the y-axis to be parallel to the normal force. Apply
![]() ††††††††††††††††††††††††††††
†††††††††††††††††††††††††††† ![]()
![]() †††††††††††††††††††††††††††††††††
††††††††††††††††††††††††††††††††† ![]()
Find the forces in the x- and y- directions and the net force in each direction:
†††††††††††
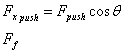 ††††††††††††††††††††††††††††
†††††††††††††††††††††††††††† 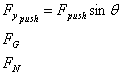
![]() ††††††††††††††††††††††††††††††
†††††††††††††††††††††††††††††† ![]()
![]() ††††††††††††††††††††††
†††††††††††††††††††††† ![]()
We are looking for Ff, which we can solve for with the equation for the net force in the x-direction.
(3) Plan the Solution: Can we find the solution?
Using the fact that ![]() = 0, we can solve for Ff:
= 0, we can solve for Ff:
![]()
(4) Execute the Plan: What is the answer?
![]()
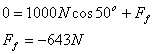
(5) Evaluate the Answer:† Can this be true?
The units are correct. The frictional force is negative, which means it is in the opposite direction to the pushing force, which makes sense.
Part (b):
(1) Focus on the Problem: Whatís going on?
Your friend pushes on a box and it doesnít move. You want to find the frictional force while he is pushing on the box. Since the box is not moving, the acceleration is zero and the net force on the box is zero. You can use the fact that the net force is zero in both the x- and y- directions to find the frictional force.
(2) Describe the Physics: What is the physics?
Draw a force diagram for the box.
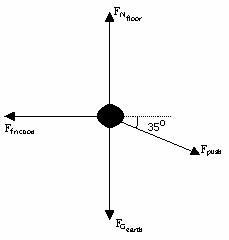
Choose the x-axis to be parallel to the frictional force and
the y-axis to be parallel to the normal force. Apply
![]() ††††††††††††††††††††††††††††
†††††††††††††††††††††††††††† ![]()
![]() †††††††††††††††††††††††††††††††††
††††††††††††††††††††††††††††††††† ![]()
Find the forces in the x- and y- directions and the net force in each direction:
†††††††††††
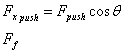 ††††††††††††††††††††††††††††
†††††††††††††††††††††††††††† 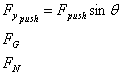
![]() ††††††††††††††††††††††††††††††
†††††††††††††††††††††††††††††† ![]()
![]() ††††††††††††††††††††††
†††††††††††††††††††††† ![]()
We are looking for Ff, which we can solve for with the equation for the net force in the x-direction.
(3) Plan the Solution: Can we find the solution?
Using the fact that ![]() = 0, we can solve for Ff:
= 0, we can solve for Ff:
![]()
(4) Execute the Plan: What is the answer?
![]()
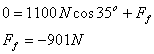
(5) Evaluate the Answer:† Can this be true?
The units are correct. The frictional force is negative, which means it is in the opposite direction to the pushing force, which makes sense.
Part (c):
(1) Focus on the Problem: Whatís going on?
Your friend and you are pushing on a box. You want to know if the box will move. You need to find the net force that you apply in the x-direction and the maximum frictional force. You need to determine if the net force you are applying in the x-direction is greater than the maximum frictional force, in which case the box would move.
(2) Describe the Physics: What is the physics?
Draw a force diagram for the box.
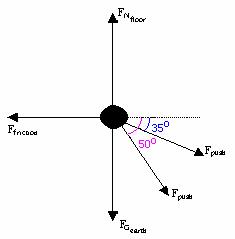
Choose the x-axis to be parallel to the frictional force and
the y-axis to be parallel to the normal force. Apply
![]()
†††††††††††††††††††††††††††††††††††
to find the normal force and the fact that the maximum frictional force is related to the normal force
![]()
to find the maximum frictional force.
Find the total force of the push in the x-direction
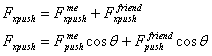
Compare it to the maximum frictional force. If the total force of the push is greater than the maximum frictional force then the box will move.
(3) Plan the Solution: Can we find the solution?
Find the forces in the y-direction, solve for the normal force and then solve for the maximum frictional force:
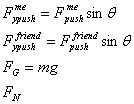
![]()
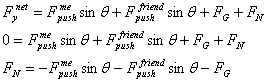
Use the equation below to find the maximum frictional force.
![]()
Find the total force of the push in the x-direction
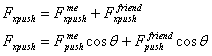
Compare it to the maximum frictional force.
†
(4) Execute the Plan: What is the answer?
Choose up as positive, so forces pointing upward will be positive and forces pointing downward will be negative.
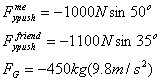
![]()
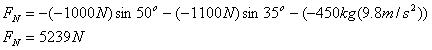
The maximum frictional force is
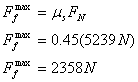
Find the total force of the push in the x-direction
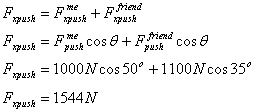
The frictional force is to the left and the force of the push is to the right. The total force of the push is less than the maximum frictional force, so the box will not move.
(5) Evaluate the Answer:† Can this be true?
It makes sense that the box would not move.