UNIT 1 READING B

Scalar

Any quantity which has a magnitude but no direction associated with it is called a scalar. For example, length, mass and temperature.

Vectors

A vector is a quantity with a magnitude and a direction that can be represented by an arrow.

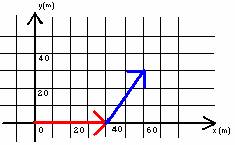
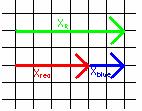
Suppose a person walks 40m directly east from the Athletic Complex, then cuts across campus 31.6m at an angle 56.3 degrees north of east, as indicated by the red and blue arrows in the diagram below.

The final position of the person is the vector represented by the green arrow in the diagram below.

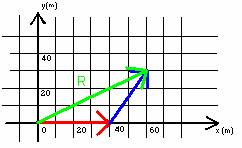
Mathematically, the green vector (arrow) is said to be the sum of the red and blue vectors (arrows).

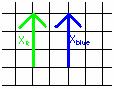
An individual vector can be considered to be the sum of a vector in the x-direction and in the y-direction, as in the picture below. The green vector in the picture can be considered to be the sum of the blue vector and the purple vector.

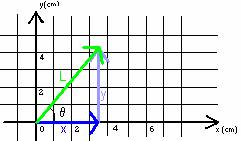
The blue vector is called the x-component of the green vector, L, and the purple vector is called the y-component of the green vector, L. If the length of a vector and the angle it makes with an axis is known then its components can be found from trigonometry. For example, if the length of the green vector is 5.4cm and it makes an angle of q = 51^o with the positive x-axis then the lengths of the blue and purple vectors can be calculated.

The following trigonometric identities for a right triangle are useful in vector problems.

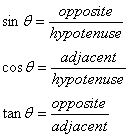
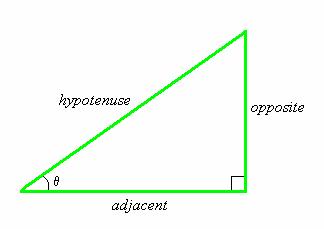
Using the above trigonometric identities for a right triangle and applying them to the above case one finds that

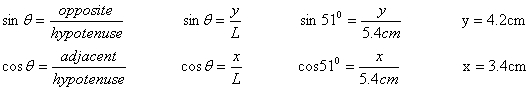
The length of the y-component (the purple vector) is 4.2cm and the length the x-component (the blue vector) is 3.4cm.

Vector Addition

There are different ways to determine the sum of two or more vectors. We will present two ways below.

Method 1)

(i) Draw the vectors you want to add with the tail of the second vector at the head of the first vector (the tail of the third vector at the head of the second vector, etc.), with the length of each vector corresponding to the length it represents at the appropriate angles.

(ii) Draw a vector from the tail of the first vector to the head of the last vector. This vector is the sum of the other vectors. It is called the resultant vector.

(iii) Measure the length of the resultant vector with a ruler and the angle it makes from a particular axis with a protractor to find its magnitude and the direction.

For example, in the diagram referred to above,

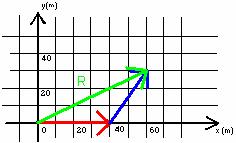
the red vector is drawn 40m long pointing east and the blue vector is drawn 31.6m long at 56.3 degrees north of east. The green vector represents the resultant vector (the sum of the red and blue vectors). The length of the green vector is 68m and the angle is 15 degrees above the positive x-axis.

Method 2) The x- and y- components of the resultant vector can be found by adding the x-components and y-components of the vectors to be summed.

(i) Find the x-components and the y-components of each of the vectors you wish to add.

(ii) Add the x-components of all the vectors. If the x-component of a vector points in the negative x-direction, it has a negative value. If the x-component of a vector points in the positive x-direction, it has a positive value. The sum of the x-components of all the vectors is the x-component of the resultant vector.

(iii) Add the y-components of all the vectors. If the y-component of a vector points in the negative y-direction, it has a negative value. If the y-component of a vector points in the positive y-direction, it has a positive value. The sum of the y-components of all the vectors is the y-component of the resultant vector.

(iv) Use trigonometry to find the magnitude and direction of the resultant vector.

For example, in the diagram referred to above,

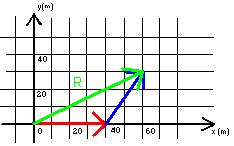
(i) For the red vector:

x_red = 40m y_red = 0m

For the blue vector, by trigonometry:

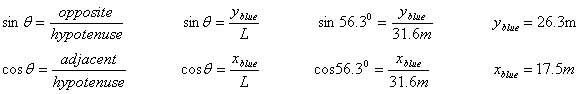
x_blue = 26.3m y_blue = 17.5m

(ii)

(iii)

(iv) The magnitude of the resultant is found by trigonometry.

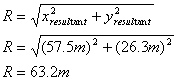
We choose to find the angle the resultant vector makes with the x-axis.

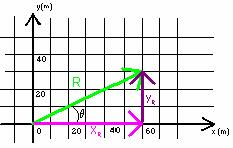
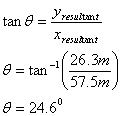
The resultant is 63.2m at an angle of 24.6^o above the x-axis.

Vector Subtraction

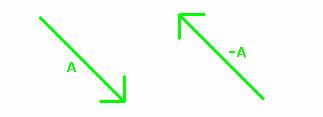
To subtract one vector from another is the same thing as adding the negative of the second vector to the first. The negative of a vector is a vector of the same magnitude as the vector, but pointing in the opposite direction.

For example, the negative of vector A is the vector –A as shown in the diagram below.

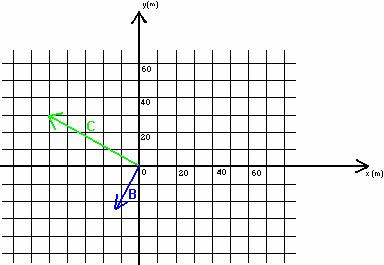
For example, consider subtracting vector B from vector C in the diagram below. Vector B has a magnitude of 27m and makes an angle of 25^o with the negative y-axis. Vector C has a magnitude of 58.3m and makes an angle of 59^o with the positive y-axis.

This is equivalent to adding the negative of vector B to vector C as in the diagram below.

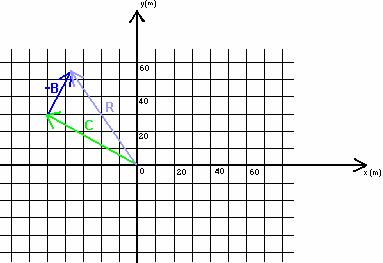
To calculate the resultant vector:

(i) For the vector -B:

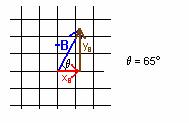
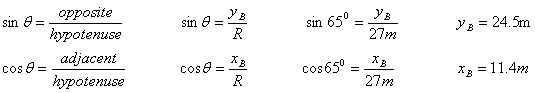
For the vector C:

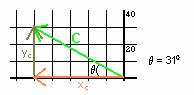
Using trigonometry, we can find the magnitudes of the x- and y- components of the vector C.

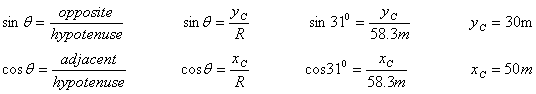
From the drawing we know that x_C is in the negative x-direction, so x_C = -50m. So when we add x_C and x_B as vectors, we use a minus sign to take into account the fact that the vector x_C points in the opposite direction to the vector x_B.

(ii)

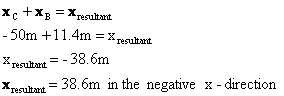
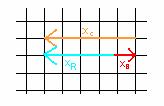
(iii)

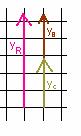
(iv) The magnitude of the resultant is found by trigonometry.

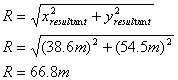
We choose to calculate the angle shown in the diagram below.

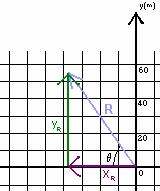
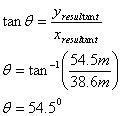
The resultant is 66.8m at an angle of 54.5^o above the -x-axis.

Example 2: Add the three vectors shown in the diagram below. The blue vector has a magnitude 1.5m and is 40 degrees from the y-axis. The red vector has a magnitude 4m and is at a 20 degrees angle below the x-axis. The green vector has a magnitude 6m and is at a 56 degree angle to the – y-axis.

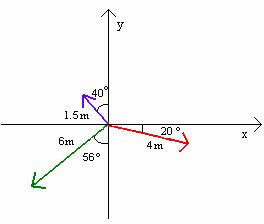
To calculate the resultant vector:

(i) For the blue vector:

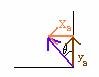
From the drawing we know that x_B is in the negative x-direction, so x_B = -0.96m. So when we add x_B to the other vectors, we use a minus sign to take into account the fact that the vector x_B points in the negative direction.

For the red vector:

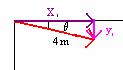
From the drawing we know that y_r is in the negative y-direction, so y_r = -1.4m. So when we add y_r to the other vectors, we use a minus sign to take into account the fact that the vector y_r points in the negative direction.

For the green vector:

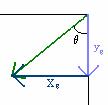
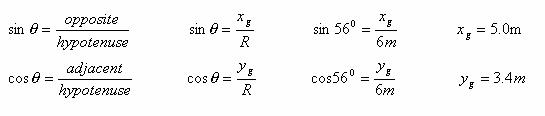
From the drawing we know that both x_g and y_g are in the negative direction, so x_g = -5.0m and y_g = -3.4m. So when we add x_g and y_g to the other vectors, we use a minus sign to take into account the fact that they point in the negative direction.

(ii)

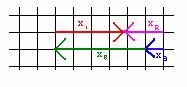
(iii)

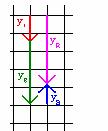
(iv) The magnitude of the resultant is found by trigonometry.

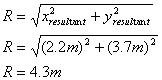
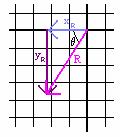
We choose to calculate the angle shown in the diagram below.

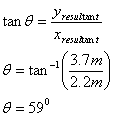
The resultant is 4.3m at an angle of 59^o below the -x-axis.