UNIT 16
ROTATIONAL
DYNAMICS
Objectives
- To understand the relationship between net torque and angular acceleration.
- To understand the concept of the moment of inertia.
- To understand the concept of angular momentum.
- To understand that the angular momentum is conserved if there is zero net torque.
- To understand the relationship between net torque and angular momentum.
Equipment:
††††††††††† 1 rotary motion sensor
††††††††††† 1 rotational accessory
††††††††††† string
††††††††††† 1 small set of hanging masses
††††††††††† 1 rod
††††††††††† 1 rod stand
††††††††††† 1 ring and disk set
††††††††††† LoggerPro software
††††††††††† LabPro computer interface
††††††††††† Excel Program
1.1
a. How could you keep an object rotating at constant angular speed? Would you apply a force? If so, in what direction would the force be applied? Would the force be continually applied? Explain your reasoning.
b. How could you keep an object rotating at constant angular acceleration? Would you apply a force? If so, in what direction would the force be applied? Would the force be continually applied? Explain your reasoning.
Discuss your reasoning with an instructor.
c. Would there be a net torque on the object in each of the cases a and b above?
d. Could you start an object rotating with zero net torque on the object? Explain.
1.2
a. Consider two objects of equal mass and different shape. For example, consider a ring and a disk of equal mass. If the same net torque is applied to each object, would they have the same angular acceleration?
b. Set up the following experiment to test your prediction in part a.† It consists of an object mounted on a platform that is free to rotate. A torque can be applied to the platform by a string attached to the platform (wrapped around the base of the platform), that runs over a pulley and is connected to a mass. If the mass is released, and allowed to fall, a torque is applied to the platform.
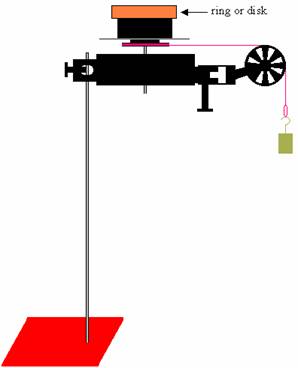
If there is very little friction on the platform, determine the net torque on the rotating platform containing the disk or ring.
c. Does the platform accelerate at the same rate with the same net torque applied, if the ring is on top as is if the disk is on top? Explain your reasoning.
1.3
a. Using the same apparatus as in section 1.2, perform the following experiment with the ring:
- Connect the LabPro to the rotary motion sensor.
- Using LoggerPro, record the number of revolutions of the ring plus platform in 0.5 seconds for 10g, 20g, 30g, 40g and 50g masses.
- Assuming very little friction on the platform, determine the net torque on the rotating ring plus platform for each mass.
- Using rotational kinematics equations, determine the angular acceleration for each net torque.
- Using Excel plot net torque (y-axis) vs. angular acceleration (x-axis).
Is there a relationship between the net torque and the angular acceleration? Explain. Predict the mathematical relationship (if you think there is one) between net torque and angular acceleration. If you donít think there is a mathematical relationship between the net torque and the angular acceleration, explain why. If you do think there is a mathematical relationship between net torque and angular acceleration, explain your prediction of the form of the mathematical relationship.
b. Repeat part a with the disk.
Discuss your results with an instructor.
c. In parts a and b we found that the data fell in a straight. Under the Chart option choose Add Trendline. Under Type choose Linear. Under Options choose Display equation on chart and Display R-squared value on chart. Determine the slope of the line for the ring and the disk. Are the slopes the same?
The net torque and the angular acceleration are related by a constant
![]()
The constant I is called the moment of inertia. The units of the moment inertia are kgm2.
The moment of inertia is different for different objects; it depends on how mass of the object is distributed and the axis about which the object is rotating. It can be found experimentally, as you did, by measuring the net torque and angular acceleration of an object about a particular axis. It is also possible to calculate the moment of inertia about a particular axis. The moment of inertia is given mathematically by
![]()
where the ![]() †are the small pieces
of mass in which the object is composed and the
†are the small pieces
of mass in which the object is composed and the ![]() †are the distances of
the small pieces of mass to the axis of rotation. (See Unit 14 Reading A Rotational Kinamatics and Energy) The moment
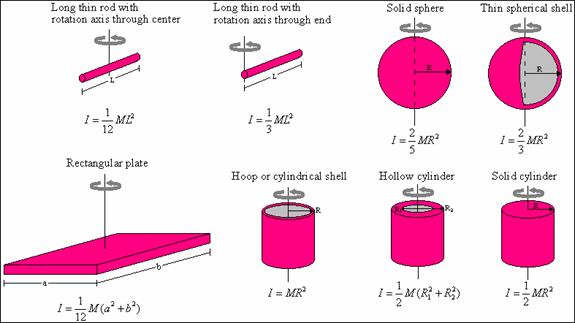
of inertia for some common objects are given below.
†are the distances of
the small pieces of mass to the axis of rotation. (See Unit 14 Reading A Rotational Kinamatics and Energy) The moment
of inertia for some common objects are given below.
Equipment:
††††††††††† 1 Rotating platform
††††††††††† 1 rotary motion sensor
††††††††††† 1 rotational accessory
††††††††††† 1 rod
††††††††††† 1 rod stand
††††††††††† 1 ring and disk set
††††††††††† LoggerPro software
††††††††††† LabPro computer interface
†††††††††††
2.1
a. Consider an object rotating with zero angular acceleration. Is there a net torque on the object? Explain?
b. Obtain a rotating platform. Have someone stand on the platform with their hands to their sides and start them spinning. After you have started them spinning, if there is very little friction on the platform, is there a net torque on the person? Is their angular speed increasing? decreasing? remaining constant? Explain your reasoning.
c. While the person is spinning, have them extend their arms out to the side. Then have them pull their arms back in. Does their angular speed change as they move their arms out? Does their angular speed change as they move their arms in?
d. While the person is spinning, does the moment of inertia change when the person extends their arms out to the side and pulls them back in?
2.2
a. We will observe another situation in which the net torque is zero, but the moment on inertia and the angular speed are allowed to change. Use the rotary motion sensor and the platform as shown below to perform the following experiment:
Start the platform spinning and then start taking position vs. time data.
After the platform has been spinning for 2 - 3 seconds, still taking data, drop the black loop on top of the spinning platform (get as close as you can to the platform before you drop it).
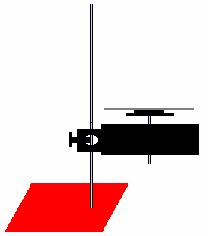
Determine the angular velocity before and after the loop was dropped onto the platform from the LoggerPro graph. Determine the moments of inertia for the platform and the loop using the examples given in 1.3.c.
Calculate the product of the total moment of inertia before the loop was dropped, I1, and the angular velocity before for the loop was dropped, w1.
Calculate the product of the total moment of inertia after the loop was dropped, I2 (the total moment of inertia can be found by adding the moment of inertia of the platform to the moment of inertia of the loop), and the angular velocity after for the loop was dropped, w2.
Compare the product of the total moment of inertia before the loop was dropped, I1, and the angular velocity before for the loop was dropped, w1, to the product of the total moment of inertia after the loop was dropped, I2, and the angular velocity after for the loop was dropped, w2.
Discuss with an instructor.
If the net torque of an object is zero, the product of the total moment of inertia and the angular velocity, Iw, is constant:
![]()
where I1 is the initial moment of inertia, I2 is the final moment of inertia, w1 is the initial angular velocity and w2 is the final angular velocity.
The product of the total moment of inertia and the angular
velocity, Iw, is called the angular
momentum, L (![]() ). If there is no net torque on an object, the angular
momentum is conserved; the initial angular momentum is equal to the final
angular momentum. This can be written as:
). If there is no net torque on an object, the angular
momentum is conserved; the initial angular momentum is equal to the final
angular momentum. This can be written as:
![]()
![]() †=
†= ![]()
Equipment:
††††††††††† 1 bicycle wheel
††††††††††† 1 rotating platform
3.1
It is possible to consider the angular velocity to be a vector quantity. The direction of the vector of the angular velocity is chosen to be perpendicular to the plane of rotation of the object and is given by the following right hand rule:
If you curl the fingers of your right hand in the direction of motion, your thumb will point in the direction of the angular velocity, as in the picture below.
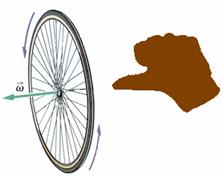
(Adapted from Physics,
James S. Walker, By Pearson Education, Inc., 2004)
This means that angular momentum is a vector quantity that points in the same direction as the angular velocity.
The net torque is in the direction in the change in the angular velocity:
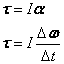
or the change in angular momentum:
![]()
Since the angular velocity and the angular momentum are along the axis of rotation, a torque applied along the axis of rotation increases or decreases the angular speed.
A torque applied perpendicular to the axis of rotation causes the axis of rotation to turn.
a. Obtain a bicycle wheel and a rotating platform. Stand on the platform holding the wheel with the handles parallel to the floor. Spin the wheel. Turn the wheel so the handles are perpendicular to the floor. What happens?
Determine the direction of the angular speed, the angular momentum and the applied torque. Is this consistent with the above equations.
SUMMARY
You should understand the relationship between net torque and angular acceleration. You should understand the concept of the moment of inertia. You should understand the concept of angular momentum. You should understand that the angular momentum is conserved if there is zero net torque. You should understand the relationship between net torque and angular momentum.