UNIT 15
ROTATION
KINEMATICS
Objectives
- to understand the concept of angular speed
- to understand the concept of angular acceleration
- to understand and be able to use kinematics equations to describe the motion of objects moving with constant angular acceleration.
This video shows a wheel chair in motion.
Equipment:
1 stopwatch
1 meterstick
1.1
a. Have one person in your group extend their arms (as in the picture below) and rotate slowly so that their fingertips move at a constant speed. Record the time it takes their arm to sweep through a known angle, q.
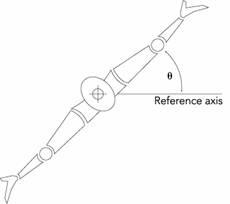
Rotating arms featuring
elbows and hands.
b. Calculate the speed of your elbow and the speed of your fingertips. Are your elbow and your fingertips moving at the same speed?
c. Is the speed of your elbow and the speed of your fingertips related to the distance of your elbow and your fingertips from the axis of rotation (the center of your body)?
d. The angle, q, through which you rotated was measured from a reference axis (as in the picture above). At any given time during the rotation, is the angle between your elbow and the reference axis different than the angle between your fingers and the reference axis? Explain.
e. You were asked in part a to rotate at constant speed, but you found two different speeds for your elbow and for your fingertips. What is meant by the term constant speed? How is this speed different from the speed of your fingertips and the speed of your elbow you calculated in part b? Explain.
Explain your reasoning to an instructor.
1.2 An understanding that angles can be measured in units of radians or units of degrees and the relationship between angles measured in radians and angles measured in degrees is critical in the study of rotational motion.
We first need to define an arc length. An arc length is the distance, s, subtended by an angle, q, along the circumference of a circle, as shown in the picture below.
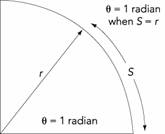
1. A degree is defined as 1/360th of a rotation in a complete circle.
2. A radian is defined as the angle for which the arc along the circle is equal to its radius. An angle measured in radians is the ratio of the arc length to the radius
![]() .
.
a. How many radians subtend an arc length of
· 2 p r, the circumference of a circle?
· p r, half the distance around a circle?
· 5m along the circumference of a circle of radius 6.5m?
b. How many radians equal
· 85°?
· 180°?
· 125°?
· 212°?
1.3
a. Using the data in part 3.1.a, and using the reference axis as q = 0, calculate the change in q divided by the change in time
![]()
for the elbow and for the fingertips. Would this quantity be the same for a point on your arm halfway between your elbow and your fingertips? For any point on your arm?
The quantity the change in q divided by the change in
time is called the angular velocity, ![]() , where the angular speed is given by
, where the angular speed is given by
![]()
and the direction is clockwise or counterclockwise. The
units of ![]() are radians per second (rad/s).
are radians per second (rad/s).
b. Does every point on a rotating object have the same angular speed? Explain.
c. In part 1.1.b, you calculated the speed of the fingertips and the elbow of a person rotating at constant angular speed. The speed you calculated is the magnitude of the velocity of the fingertips or the elbow. The velocity is tangent to the circle through which that point is moving; it is called the tangential velocity. The tangential velocity vector is shown in the diagram below. The speed you calculated is called the tangential speed.
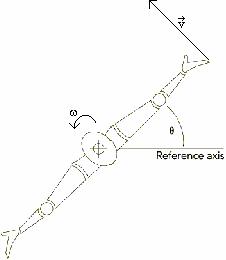
Do the fingertips and elbow have the same tangential speed? Explain.
d. Relate the tangential speed, v (the
magnitude of the tangential velocity), of the fingertips of the person in part 3.1.a
to the angular speed of the person. Write an equation relating the speed, v, to
the angular speed, ![]() .
.
Discuss your answer with an instructor.
Equipment:
None
2.1
a. Consider a rotating object that is slowing down or speeding up. Is the angular speed changing? Explain.
b. Is the tangential velocity at a point changing? Is the point accelerating? Explain.
If the tangential velocity of a point on an object is changing, the point is accelerating. Since the point is moving in a circle, there is an acceleration toward the center of the circle, as shown in the picture below. This is called the radial acceleration, aR. If the tangential speed is changing, there is also a component of the acceleration tangent to the circle through which the point is moving, as shown in the picture below. This is called the tangential acceleration, aT.
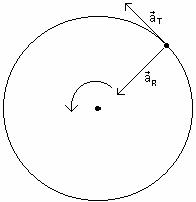
c. If the angular velocity of the rotating object is
changing, we can define an angular acceleration, ![]() . The magnitude of the angular acceleration is the change in
angular velocity divided by the change in time
. The magnitude of the angular acceleration is the change in
angular velocity divided by the change in time
![]()
and the direction is clockwise or counterclockwise. The units of angular acceleration are rad/s2. Is the angular acceleration the same for each point on a rotating object? Explain.
It can be shown that the magnitude of the angular acceleration is related to the magnitude of the tangential acceleration
![]() .
.
d. Since the angular acceleration, the angular
velocity and the angle, ![]() , is the same for all points on a rotating object, it is
often useful to work with these quantities when studying rotational motion.
, is the same for all points on a rotating object, it is
often useful to work with these quantities when studying rotational motion.
You might notice that the definitions of ![]() and
and ![]() are similar the definitions of a and v for motion in a
straight line in one dimension that we studied in Unit 1:
are similar the definitions of a and v for motion in a
straight line in one dimension that we studied in Unit 1:
![]()
![]()
![]()
![]()
It can also be shown that
![]() .
.
From these three equations, four equations for rotational kinematics can be derived, as they were for motion in a straight line. The four equations are shown below, and also the analogous equations for motion in a straight line.
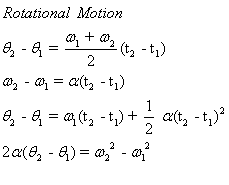
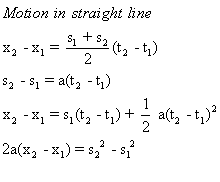
SUMMARY
You should understand the concept
of angular speed. You should understand the concept of angular acceleration.
You should understand and be able to use kinematics equations to describe the
motion of objects moving with constant angular acceleration.