UNIT 14
SIMPLE HARMONIC
MOTION
Objectives
- To understand qualitatively and mathematically simple harmonic motion
- To understand the force of a spring on an object qualitatively and mathematically
1.1
a. Obtain a kazoo. Blow on the kazoo. How does the kazoo make sound?
b. Below is a picture of a model of a larynx. The plastic represents the trachea. A strip of latex cut down the middle represents the vocal chords. Another plastic tube represents the larynx cavity. When air is blown through the tube the vocal chords vibrate as show in this movie.

Sounds are made by objects vibrating. A simple case of a vibrating object is a mass oscillating on a spring.
2.1
a. Set up a mass hanging from a spring, as shown in the picture below.
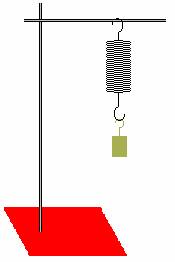
Pull the mass down a few centimeters and release it. Use a motion detector to plot graphs of position vs. time, velocity vs. time and acceleration vs. time for the oscillating mass.
The motion of a mass on a spring can be described mathematically by
![]()
where x is the position of the
mass, A is the maximum amplitude (the maximum distance from the resting position),
![]() is the angular
frequency of the motion and t is time.
is the angular
frequency of the motion and t is time.
b. The angular frequency is related to the frequency and the period as in the equations below
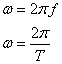
Determine the angular frequency of the mass on your spring.
c. The velocity and the acceleration of the mass on the spring can also be described mathematically by
![]()
Is this consistent with your observations? Explain.
At what point of the motion is the velocity the greatest? The least?
At what point of the motion is the acceleration the greatest? The least?
Discuss with an instructor.
3.1
a. When the mass is oscillating, is the force of the spring on the mass constant or is it changing? Explain your reasoning. If the force is not constant, what might the force of the spring depend on? Explain.
b. It is possible to measure the force of the spring on the mass when the mass is at rest. By hanging a mass from a spring, the force of the spring on the mass at a particular distance from the unstretched position can be measured. Consider the following data, and determine if the force of the spring on a mass depends on the distance of the spring from the unstretched position.
|
Spring #1 |
|
|
Spring #2 |
|
|
mass (kg) |
displacement (distance from the
unstreched position) (m) |
|
mass (kg) |
displacement (distance from the
unstreched position) (m) |
|
0.01 |
0.029 |
|
0.02 |
0.004 |
|
0.02 |
0.062 |
|
0.05 |
0.011 |
|
0.03 |
0.095 |
|
0.07 |
0.014 |
|
0.04 |
0.128 |
|
0.1 |
0.02 |
|
0.05 |
0.16 |
|
0.15 |
0.031 |
|
0.06 |
0.195 |
|
0.2 |
0.04 |
|
0.07 |
0.227 |
|
0.25 |
0.05 |
|
|
|
|
0.3 |
0.061 |
Determine a mathematical equation for the force of the spring in each case.
Discuss with an instructor.
The force of a spring on a mass is
![]()
where x is the displacement from the equilibrium position and k is a constant, called the spring constant. The units of k are kg/s2.
c. Is k the same for all springs? Explain.
The spring force, like the gravitational force, is a conservative force. A potential energy can be defined, because the work done by the spring in moving a distance xf – xi is independent of the path; it depends only on the endpoints. It can be shown with calculus that the work done by a spring in moving from xf to xi is
![]()
A spring potential energy can be defined as
![]()
The total energy of a mass on a spring is then
![]()
SUMMARY
You should understand qualitatively and mathematically simple harmonic motion. You should understand the force of a spring on an object qualitatively and mathematically.