UNIT 12
WAVES
(Sections 4.1 and 4.2 of
this unit are taken from Lillian C. McDermott, Peter S. Shaffer and the Physics
Education Group, Tutorials in Introductory Physics, Prentice Hall, NJ,
1998)
Objectives
· To understand how to create a wave
pulse
· To understand the superposition of
wave pulses
· To understand how to create a periodic
wave
· To understand the concepts of
wavelength, period, frequency and wave number as applied to a periodic wave
· To understand the mathematical
representation of a sinusoidal waveform
· To understand the superposition of
periodic waves – to understand interference
· To understand that light exhibits
wavelike behavior
1.1
a. Watch the videoclip. Describe what happened in the videoclip.
b. Watch the videoclip. Describe what happened in the videoclip.
c. We will start our study of waves by studying a pulse moving down a spring. There are two ways to create a pulse down a spring. The pulse can move perpendicular to the spring, as in part a; this is called a transverse pulse. The pulse can move in the same direction as the spring, as in part b; this is called a longitudinal pulse.
d. Consider a transverse pulse moving down a spring. Describe how you could create a transverse pulse. How would you create pulses of different amplitudes? Different widths? Different shapes?
e. Watch the videoclip again. Describe the motion of a point on the spring. If you were to mark one point on the spring, would it return to its original position after the pulse passes? Or would it be in a different position?
Discuss your answer with an instructor.
f. How would you measure the speed of a pulse on a spring? Measure the speed of the pulse in part a. You may want to open the videoclip pulse in Videopoint.
2.1
a. Consider two pulses moving in opposite directions along a spring, pulse A and pulse B, as in the picture below. Both pulses have a speed 2.00cm/s. The pulses have different heights. The picture shows the pulses at time t = 0s. Sketch the shape of the spring at the following times: 1s, 1.5s, 2.0s, 2.5s, and 3s.
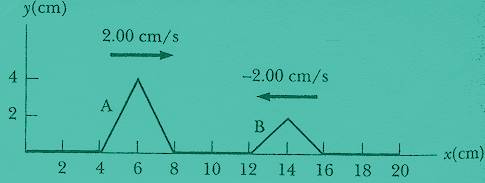
(from Raymond A. Serway and
Robert J. Beichner, Physics for Scientist and Engineers 5Th
Edition,
b. Watch the following videoclips: videoclip1, videoclip2, videoclip 3, videoclip4 and videoclip5. Discuss the shape of the spring when the two pulses overlap. Is the shape of the spring the superposition of the two pulses? Explain.
c. Consider two pulses moving in opposite directions along a spring, pulse A and pulse B, as in the picture below. Both pulses have a speed 2.00cm/s. The pulses have the same height. The picture shows the pulses at time t = 0s. Sketch the shape of the spring at the following times: 1s, 1.5s, 2.0s, 2.5s, and 3s.
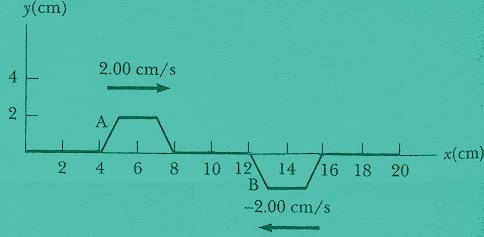
(from Raymond A. Serway and Robert
J. Beichner, Physics for Scientist and Engineers 5Th Edition,
When two or more pulses are moving along a spring, the amplitude of the spring at each point is the superposition of the amplitudes of all the pulses at that point.
d. Examine the pictures you drew in part a and c make sure they are consistent with the above statement.
Discuss your pictures with an instructor.
3.1 A wave is a disturbance that travels through a medium.
a. By continually moving the end of a spring in the same way, you could produce a waveform that repeats. The wave could appear as shown in the following animation.
Describe the motion of the piece of spring at position x = 0.
Discuss with an instructor.
Plot the amplitude of the piece of string at x = 0 as a function of time.
b. If you took a snapshot of the wave at one point in time, it would look like this:
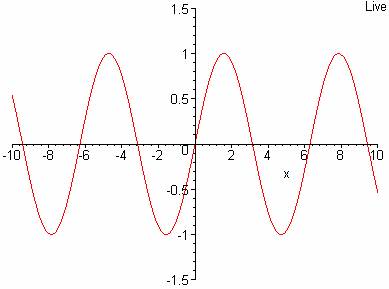
If the shape of the wave repeats, the wave is called a periodic wave. The distance over which the wave repeats itself is called the wavelength. The symbol l is used for wavelength. Determine the wavelength of the wave in the picture above. (Assume the axis of the graph is in centimeters.)
c. At a later instant in time, the wave shown in part b would look like this:
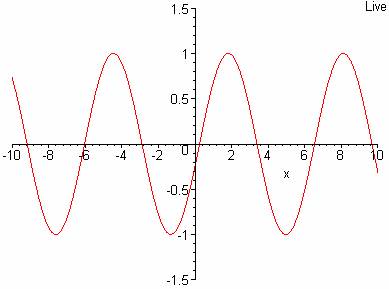
The period of a wave is defined as the time it takes for a point on the spring to go through one oscillation. The symbol T is used for period. Determine the period of the wave shown in the animation in part a.
The frequency is the number of cycles a wave completes in one second. The symbol f is used for frequency. Determine the frequency of the wave shown in the animation in part a.
The frequency is the inverse of the period:
Check and see if this agrees with your measurements.
d. From your measurements, determine the velocity of the wave in part a.
The velocity of a wave can be determined by dividing the wavelength by the period. This is equivalent to multiplying the wavelength by the frequency:
Check and see if this agrees with your determination of the velocity.
e. The maximum displacement of a piece of the spring from its resting position is called the amplitude of the wave. Determine the amplitude of the wave in part a.
3.2
A special case of a periodic waveform in one-dimension, like a wave on a string or a spring, is a wave that has a sinusoidal shape, as the wave in part 3.1.a. A sinusoidal waveform can be represented mathematically by the following equation:
where k is a constant equal to 
, 
is a constant equal to
, and A is the maximum amplitude. k is called the wave
number and is the angular
frequency. y is the amplitude of the wave at position x and at time t.
a. Write the mathematical equation for the wave in part 3.1.a with the numerical values for the maximum amplitude, A, wave number, k, and angular frequency, f.
b. Determine the amplitude of the wave in part 3.1.a at position x = 2.4cm and time t = 0.0.
4.1
Waves can travel through many different media.
a. It is possible to make periodic circular waves in water by tapping the surface of the water as in the following video.
A periodic circular wave may be represented at a moment in time by the diagram below. The dark circles represent the crests of the wave and the dashed circles represent the troughs of the wave.
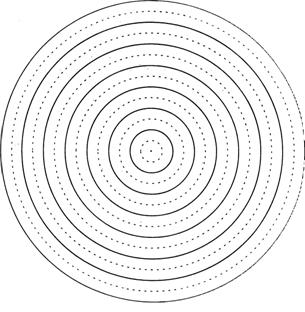
(from Lillian C. McDermott,
Peter S. Shaffer and the Physics Education Group, Tutorials in Introductory
Physics, Prentice Hall, NJ, 1998)
Two wave sources might be placed in the same tank as represented in the animation (from http://surendranath.tripod.com/Interference/Ripint.html) and in the diagram below.
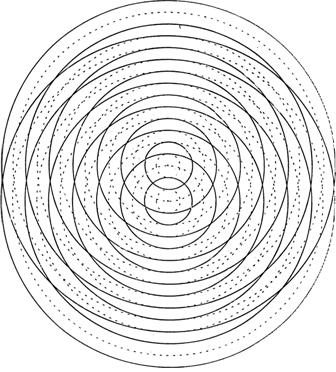
(from Lillian C. McDermott, Peter S. Shaffer and the Physics Education Group, Tutorials in Introductory Physics, Prentice Hall, NJ, 1998)
A larger version of the picture shown above can be found at the end of the unit. It is called Sheet 1. Print out Sheet 1.
(i) The sources are considered to be in-phase, if each one emits a crest at the same time, otherwise the sources are considered to be out-of-phase. Are the sources in the picture in-phase or out-of-phase?
(ii) Are the frequencies of the waves emitted by each of the sources the same or different? Explain your reasoning.
b. Referring to Sheet 1, answer the following questions:
If both of the waves have the same amplitude, describe what happens at a point on the surface of the water where
· A crest meets a crest
· A trough meets a trough
· A crest meets a trough
How would your answers to each of the questions above differ, if the waves did not have the same amplitude?
Sheet 1 represents the waves at one instant in time. Assume that the waves on Sheet 1
have the same amplitude. Use different symbols (or different colors) to mark the places at
which for the instant shown:
· The displacement of the water surface is zero (at its equilibrium level)
· The displacement of the water surface is the greatest above equilibrium
· The displacement of the water surface is the greatest below equilibrium
What patterns do you notice? Sketch the patterns on Sheet 1.
c. Consider a point on Sheet 1 where a crest meets a crest. How would the displacement of the water surface at this point change over time? Explain.
Consider a point on Sheet 1 where a crest meets a trough. How would the displacement of the water surface at this point change over time? Explain.
d. Choose a few points on Sheet 1 where the water
remains undisturbed. For each of the points, determine the distance (in terms
of the number of wavelengths) from each source. The difference in the distance
from each source is called DD. For example, if the distance of the point from source
1 is 1 wavelength and distance of the point from source 2 is 1 ½ wavelengths,
then DD
is ½ wavelength.
For points where the water level remains undisturbed,
possible values of DD
are 
Explain why this is
true in terms of superposition of waves.
Indicate on Sheet 1 all of the points that have the same value of DD.
e. Choose a few points on Sheet 1 where the water a crest meets a crest or a trough meets a trough. For each of the points, determine the distance (in terms of the number of wavelengths) from each source.
For points where a crest meets a crest or a trough meets a trough, possible values of DD are 1, 2, 3,… Explain why this is true in terms of superposition of waves.
Indicate on Sheet 1 all of the points that have the same value of DD.
f. Points where a crest meets a crest or trough meets
a trough are called points of maximum constructive interference. Points where
the water surface remains undisturbed are called nodes. A collection of points
with integer numbers of DD are called lines of maximum constructive interference.
A collection of points with DD = are called nodal
lines.
Look at the animation (from http://surendranath.tripod.com/Interference/Ripint.html). In the animation, move the sources apart. In particular, observe the lines of maximum constructive interference and nodal lines for source separations of 1, 2, 3,… wavelengths.
4.2
a. Consider the following pictures of water waves incident on slits of various widths.
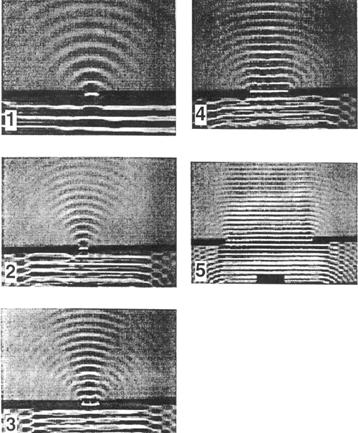
(from A. Arons, The
Various Language; an Inquiry Approach to the Physical Sciences,
In which picture does the slit act most like a source of circular water waves?
In which picture does the slit act least like a source of circular water waves?
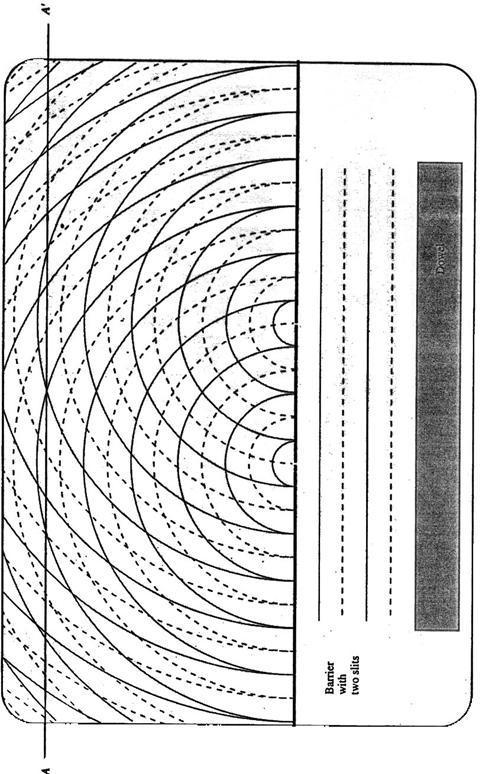
b. Consider a water wave incident on two very narrow slits, as in the picture below. The distance between the centers of the slits is 3l. The line between A and A’ represents a wall.
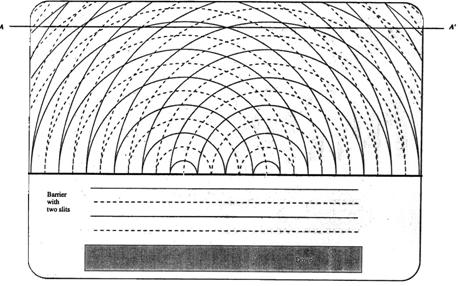
(from Lillian C. McDermott, Peter S. Shaffer and the Physics Education Group, Tutorials in Introductory Physics, Prentice Hall, NJ, 1998)
Print out the enlargement of the picture (Sheet 2) at the end of the unit. Mark the lines of maximum constructive interference and nodal lines on Sheet 2.
Describe the motion of a piece of paper placed at the intersection of a nodal line and the wall.
Describe the motion of a piece of paper placed at the intersection of a line of maximum constructive interference and the wall.
Equipment:
1 laser
1 slitfilm demonstrator
1 rod stand
1 rod
1 angle clamp
1 lens holder
1 optic stand
1 meterstick
5.1
a. Set up a laser to shine through one of the double slit patterns on the slitfilm demonstrator onto the wall, as shown in the picture below. Information on the slits is found in the literature accompanying the slitfilm demonstrator.
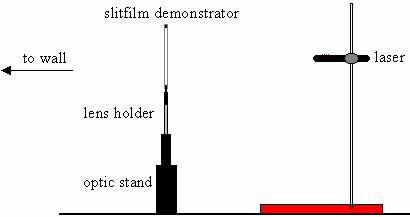
Compare the pattern on the wall with the pattern of periodic circular water waves on the wall in part 4.2.b. Are the patterns similar or are they different? Explain.
What does the comparison of the patterns tell you about the nature of light?
The interference pattern that appears on a screen when light of a single frequency is sent through two slits is evidence that light is a wave.
b. It can be shown that when the wall is very far away from the slits, the difference in the distance from each source, DD, is equal to the distance between the slits times the sin of an angle between a line drawn from the center of the slits to the wall and a line drawn from the center of the slits to a point of constructive interference or a point of destructive interference, as shown in the diagram below. If point P is a point of constructive interference,
where m is an integer and m = 1 if point P is the first point of constructive interference from the central maximum, m = 2 if point P is the second point of constructive interference from the central maximum, etc.
If point P is a point of destructive interference,
where m is an integer and m = 0 if point P is the first point of destructive interference from the central maximum, m = 1 if point P is the second point of destructive interference from the central maximum, etc.
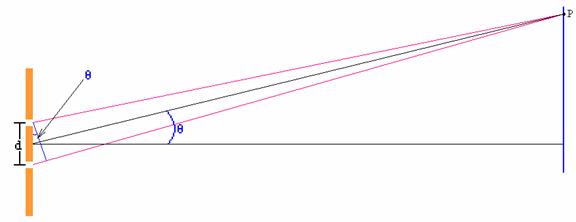
Determine the wavelength of the laser you used in part a.
Further experiments (that we will not do), have determined
that the speed of light is
and that there are many other waves that travel at besides visible light: radio waves, microwaves, infrared,
ultraviolet rays, X-rays, gamma rays. Further measurements have determined the
frequency and wavelength of these waves:
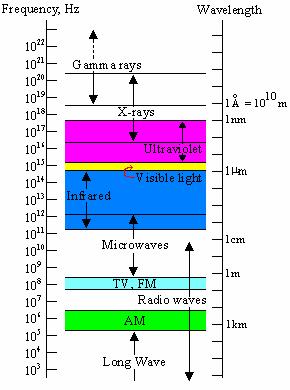
Many different frequencies of waves have medical applications.
SUMMARY
You should understand how to create a wave pulse and a periodic wave.
You should understand the concepts of wavelength, period, frequency and wave
number as applied to a periodic wave and the mathematical representation of a
sinusoidal wave. You should understand the concept of the superposition of
waves. You should understand that light exhibits wavelike behavior
Sheet 1
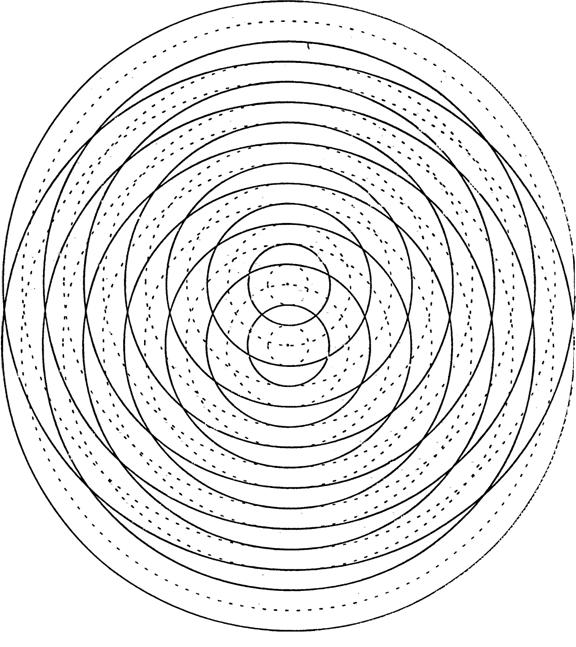
(from Lillian C. McDermott, Peter S. Shaffer and the Physics Education Group, Tutorials in Introductory Physics, Prentice Hall, NJ, 1998)
Sheet 2
(from Lillian C. McDermott, Peter S. Shaffer and the Physics Education Group, Tutorials in Introductory Physics, Prentice Hall, NJ, 1998)