UNIT 11
FLUIDS
Objectives
- To understand the concept of pressure
- To understand that for static fluids the pressure at any point in a fluid is the same in all directions and that the pressure at a particular point depends on the depth
- To be able to calculate the pressure at a depth h below the surface of a fluid at rest
- To understand that if the pressure at any point in an enclosed fluid at rest is changed, the pressure is changed by an equal amount at all points in the enclosed fluid (Pascal's Law)
- To understand the concepts of volume and density
- To understand that there is a buoyant force on a body immersed in a fluid
- To be able to calculate the buoyant force
- To understand that whether an object sinks or floats depends on the density of the object and the density of the fluid in which it is immersed
- To understand the concept of mass flow rate
- To understand the concept of volume flow rate
- To understand the continuity equation both qualitatively and quantitatively
- To
understand Bernoulliís Theorem both qualitatively and quantitatively
- To
understand how a pump works
- To understand the concept of resistance in dynamic fluid systems
- To understand the relationship between volume flow rate, resistance and pressure in dynamic fluid systems
- To understand the circulatory and respiratory systems in terms of simple models of fluid flow
Equipment:
††††††††††† Clay
††††††††††† 1 meterstick
††††††††††† 1 balance
1.1 Take a piece of clay. Form it into a block with one side about 8cm long and the other two sides about 1cm long. Stand the block on a table, as in the picture below.
![]()
a. Is a force exerted by the block on the table? If it is, determine the magnitude of the force exerted by the block on the table. Explain your reasoning.
b. Rotate the block, as in the picture below. Is a force exerted by the block on the table? If it is, determine the magnitude of the force exerted by the block on the table. Explain your reasoning.
![]()
c. Is the force exerted by the block on the table exerted at one point on the table? Or is it a force exerted by the block at different points along the table? Explain your reasoning.
d. Suppose you had a wedge of clay resting on a table, as in the diagram below.
![]()
![]()
Would the force exerted by the clay on the table be the same at all points? Explain your reasoning.
e. In the three cases above, would it make sense to speak of a force per unit area? Explain.
f.† In each of the cases above, would you say that the force per unit area is constant? Explain.
g. Determine the force per unit area for the blocks in parts a and b above. Show your calculation.
h. In which case is the force per unit area greatest?
i. Consider the two pictures below. In each case, the force applied is the same. In one case, the force is applied by a finger, in the other case, the part touching the skin is a needle. Which would hurt more? Explain.
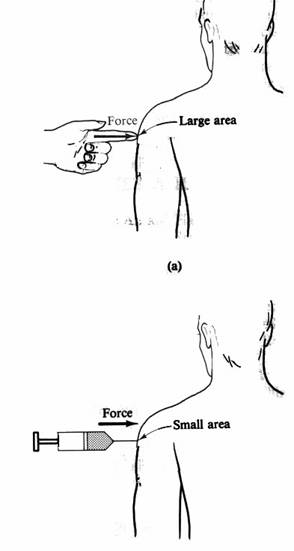
(from Physics with Health Science Applications by Paul Peter Urone, John Wiley and Sons, NY, 1986)
Pressure is defined as the force per unit area. Mathematically,
![]()
The unit of pressure is a Pascal. One Pascal is one N/m2.
Equipment:
††††††††††† None
2.1
a. Define fluid in your own words.
b. Is a liquid a fluid? Is a gas a fluid? Explain your reasoning.
A fluid is a continuous substance, lacking a definite
shape, which has a tendency to assume the shape of its container. Both gases
and liquids are fluids.
Equipment:
††††††††††† 1 beaker
††††††††††† 1 1000mL graduated cylinder
††††††††††† 1 tall cylinder with three holes in the side
††††††††††† LoggerPro software
††††††††††† LabPro computer interface
††††††††††† 1 force sensors
††††††††††† 1 gas pressure sensor
3.1 Fill a beaker with water.
a. Calculate the pressure of the water on the bottom of the beaker.
b.† Consider a beaker full of water, as in the picture below. Height A is 1/3 the distance from the top of the beaker and height B is 2/3 the distance from the top of the beaker. Is the pressure the same at heights A and B? Explain.
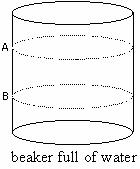
c. Calculate the pressure at heights A and B due to the water above that height.
d. Obtain a tall cylinder, with holes at different heights from the bottom of the cylinder and a force sensor at each hole. Each of the holes is the same area. Pour water into the cylinder. Measure the force per unit area at each of the holes, using the LabPro computer interface Is the pressure (force per unit area) on the wall of the container the same at different heights from the bottom of the container? Explain your reasoning.
e. Obtain the 1000mL graduated cylinder and fill it with water. Measure the pressure at three different levels with the gas pressure sensor, using the LabPro computer interface and the file pressure vs. time.
f. At a fixed level in the graduated cylinder, measure the pressure in different directions (up, down, to the side). Is the pressure the same in all directions?
Pascal said that the pressure at any point in a fluid is the same in all directions and that the pressure at a particular point depends on the depth.
h. Is Pascalís statement consistent with what you found in parts d, e, and f above? Explain.
Equipment:
††††††††††† 1 hydraulic lift apparatus
††††††††††† 1 mass set
4.1 Pascal also said that if the pressure at any point in an enclosed fluid at rest is changed, the pressure is changed by an equal amount at all points in the enclosed fluid. This is known as Pascalís Law.
a. Obtain a hydraulic lift apparatus that consists of a large cylinder and a small cylinder connected by a tube filled with a liquid, as in the diagram below. Apply a known amount of force to the large cylinder.
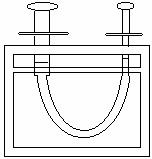
If Pascalís Law is true, calculate the force on the piston in the small cylinder. Show your work.
Show your result to an instructor.
This is the concept behind a hydraulic lift.
Equipment:
††††††††††† None†††††††††††††††††††††††††††
5.1
a. Write a qualitative definition of volume.
b. Describe what happens when you place an object in a container of water. Could you use this to write an operational definition of finding the volume of an object?
c. Write an operational definition for finding the volume of an object.
Show your definition to an instructor.
Equipment:
††††††††††† 2 pieces of aluminum
††††††††††† Several objects that sink and float
††††††††††† 1 balance
††††††††††† 1 mass set
††††††††††† 1 beaker
†††††††††††
6.1
a. Give a qualitative explanation of density. (This should be an explanation in your own words.)
The density of an object is defined as its mass divided by its volume
![]() .
.
The symbol ![]() †is used for density.
The units of density are kg/m3.
†is used for density.
The units of density are kg/m3.
Is this consistent with your qualitative explanation? Explain.
b. Do 30ml of water have the same density as 50ml of water? As 28ml of water? Explain. Do objects made of the same material have the same density? Do two pieces of aluminum have the same density? (Test it.) Two pieces of wood? Explain.
c. Compare the densities of sinking objects to the density of the liquid in which the objects are immersed.† What would happen to an object that had exactly the same density as the liquid in which it was immersed?
Equipment:
††††††††††† Several objects that sink and float
††††††††††† 1 balance
††††††††††† 1 mass set
††††††††††† 1 spring scale
††††††††††† 1 beaker
††††††††††† string
†††††††††††
7.1
a. Obtain one object that sinks in water. Use a balance to determine the mass of the object. Find the volume of the object. Suspend the object in water, using a string attached to a spring scale, as in the diagram below.
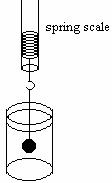
(i) Draw a force diagram for the object.
(ii) Determine the upward force on the object due to the spring and the gravitational force on the object. If there are any other forces acting, determine the magnitude of those forces.
Discuss your answers with an instructor.
The upward force on a body due to the water in which it is immersed, is called the buoyant force.
b. Determine the mass, volume, and weight of the displaced water for the object. Compare the buoyant force on the object to the mass, volume, and weight of the displaced water. Are any of the quantities roughly the same?
Archimedesí principle states that the buoyant force on a body immersed in a fluid is equal to the weight of the fluid displaced. This can be written mathematically as
![]()
where ![]() †is the buoyant force,
mF is the mass of the fluid, g = 9.8m/s2
†is the buoyant force,
mF is the mass of the fluid, g = 9.8m/s2
or
![]()
where ![]() †is the
buoyant force, rF
is the density of the fluid, VF is the volume the fluid and g =
9.8m/s2.
†is the
buoyant force, rF
is the density of the fluid, VF is the volume the fluid and g =
9.8m/s2.
Is Archimedesí principle consistent with your data?
c. If you were to cut the string in part a, what would happen to the objects? Would the buoyant force change? Explain.
d. Obtain one object that floats in water. Use a balance to determine the mass of the object. Find the volume of the object. Test the hypothesis that Archimedesí principle also holds true for floating objects. In other words, determine if the buoyant force on a floating object is equal to the weight of the displaced liquid. Design an experiment to do this and carry it out.†
e. Draw a force diagram for a floating object and use it to explain why objects that are less dense than a liquid float in the liquid.
Explain your experiment and the results to an instructor.
Equipment:
††††††††††† 1 clear plastic rectangular container
††††††††††† 1 beaker
†††††††††††
8.1
a. Obtain a rectangular container made of clear plastic. Fill the container with 5cm of water. Calculate the pressure on the bottom of the container due to the water above it.
b. Calculate the pressure at a depth, h, below the surface of the water, due to the water above it. Write your final answer in terms of the density of water, the acceleration due to gravity, g, and the depth, h.
Is this consistent with your answer to parts 3.1.c above? Explain.
c. Fill a graduated cylinder or beaker. Calculate the pressure at a depth, h, below the surface of the water. Write your final answer in terms of the density of water, the acceleration due to gravity, g, and the depth, h.
d. Use a pressure sensor to test your calculations in parts b and c.†
Check your equations with an instructor.†
e. Would the pressure at a depth, h, below the surface of the liquid be the same in two different containers, both filled with water? Explain.
For a fluid that is not flowing, a static fluid, the pressure at a depth h below the surface of the fluid is
![]()
This is called the hydrostatic equation. The pressure below the surface of a fluid depends only on the depth h below the surface of the fluid, not on the shape of the container.
f. Would the pressure at a depth, h, below the surface of the liquid be the same in two different containers, if the containers had different liquids in them? Explain.
Up to this point we have been talking about static fluids,
fluids that are not flowing. Now we are going to study flowing fluids. This is
called fluid dynamics.
Equipment:
††††††††††† 1 Garden hose
9.1
a. Obtain a garden hose. Hold the end of the hose horizontally, turn the water on and observe the water leaving the hose.
Use your finger to cover part of the opening at the end of the hose. Observe the water leaving the hose. Can you make any statements about the velocity of the water leaving the hose when it is covered with your finger compared to the velocity of the water leaving the hose when the opening is not partially covered by your finger based on your observations? Explain.
b. If you had two tubes of different radii attached to make one tube, as in the diagram below, and water was flowing through the tubes, would the water flow at the same velocity through the narrow part as through the wider part? Explain.
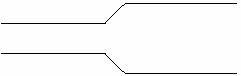
9.2 The amount of mass per unit time passing a cross-sectional area, A, of a pipe is called the mass flow rate.
a. Consider a pipe that consists of two parts, one with a wider cross-sectional area, as shown in the diagram below.
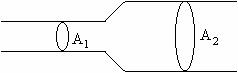
Consider the following statement, which refers to the above diagram:
If the liquid flowing does
not build up in the pipe between area A1 and area A2,
then the mass per unit time passing cross-sectional area A1 must
equal the mass per unit time passing cross-sectional area A2.
Discuss this statement with your group members and see if they agree.
If this statement is true, would the velocity of the fluid be the same when it crosses area A1 as when it crosses area A2? Or would the velocity of the fluid as it crosses area A1 be greater or less than the velocity of the fluid as it crosses area A2? Explain.
Is this consistent with your answer to parts a and b?
b. What factors do you expect the mass per unit time passing a cross-sectional area, the mass flow rate, to depend on? List the factors. Explain.
c. The mass flow rate can be written mathematically as
![]()
where Dm is the amount of mass passing a cross-sectional area, A, in a time Dt.
The mathematical derivation of the mass flow rate is shown in Unit 11 Reading A.
The mass flow rate can be defined mathematically as
†![]() .
.
The mass flow rate, the mass per unit time passing a cross-sectional area A1, depends on the area, A1, the velocity of the fluid in the pipe as it crosses area A1 (v1), and the density of the fluid.
†
f. If the mass flow rate is the same in each part of the pipe (the fluid is non-compressible) shown in the picture above, then
![]()
and
![]()
This is a mathematical statement of the continuity equation.
The continuity equation states that the velocity of a liquid flowing through a narrower part of a pipe is greater than the velocity of liquid flowing through a wider part of a pipe.
Equipment:
††††††††††† 1 Venturi
tube
10.1
a. Obtain a Venturi tube. It consists of a horizontal tube that is wide at each end and narrow in the middle. There are vertical tubes attached to the narrow and wider sections of the horizontal tube.† Flow water through the Venturi tube and observe the height of the water in the vertical tubes attached to the horizontal tube. What do your observations about the height of the water indicate about the pressure in the each part of the horizontal tube? Explain your reasoning. Where is the pressure greater, where is it less? Is the velocity of the fluid the same in each part of the tube?
b. Take a sheet of paper about 4 ī 6 in. and blow across the top of it. Which direction does the paper move? Is the force per unit area (pressure) greater on top of the paper or below the paper? Is the velocity of air greater above the paper or below the paper?
c. How is the pressure related to the velocity of the fluid? (Is the pressure higher where the velocity is higher? Qualitatively, what is the relationship between velocity and pressure?) Explain.
Bernoulliís Theorem states that
![]()
where the subscript 1 refers to the part of the tube with area A1 and the subscript 2 refers to the part of the tube with area A2, so p1 is the pressure in the tube at height h1 with area A1, p2 is the pressure in the tube at height h2 with area A2, v1 is the velocity in the tube at height h1 with area A1, v2 is the velocity in the tube at height h2 with area A2. Bernoulliís Theorem is only true if energy is conserved (if there is no loss due to friction).
If both parts of the pipe are at the same level, then ![]() †and
†and
![]()
d. Is the mathematical equation consistent with your observations in parts a and b? Explain.
Equipment:
††††††††††† 1 Hydraulic lift pump
††††††††††† 1 force pump
11.1 One way to get fluid to flow is to push on it. A pump is a mechanism for doing just this.
a. Examine a hydraulic lift pump. Explain what happens when the piston is raised and lowered. Examine the valves. Explain how the pump works in terms of pressure and other concepts you have learned.
b. The heart works like two force pumps. Examine a force pump. Explain what happens when the piston is raised and lowered. Examine the valves. Explain how the pump works in terms of pressure and other concepts you have learned.
Equipment:
††††††††††† 1 5 gallon bucket with hole†
††††††††††† 2 1 gallon bucket without holes
††††††††††† 1 40cm long copper pipe with 0.6cm radius with stopper
1 40cm long copper pipe with 0.5cm radius with stopper
1 40cm long copper pipe with 0.37cm radius with stopper
1 40cm long copper pipe with 0.2cm radius with stopper
1 20cm long copper pipe with 0.2cm radius with stopper
1 7.5cm long copper pipe with 0.2cm radius with stopper
1 15cm long copper pipe with 0.2cm radius with stopper
1 22.5cm long copper pipe with 0.2cm radius with stopper
1 30cm long copper pipe with 0.2cm radius with stopper
1 37.5cm long copper pipe with 0.2cm radius with stopper
1 45cm long copper pipe with 0.2cm radius with stopper
1 52.5cm long copper pipe with 0.2cm radius with stopper††
1 stopwatch
††††††††††† 1 500 mL graduated cylinder
††††††††††† 1 Excel program
††††††††††† water
12.1 The volume flow rate is the volume of fluid passing a cross-sectional area, A, in a time Dt. The volume flow rate is the velocity times the area
![]()
It is related to the mass flow rate given above as follows
![]()
a.† Consider a 5 gallon bucket with a pipe attached to it as in the picture below.
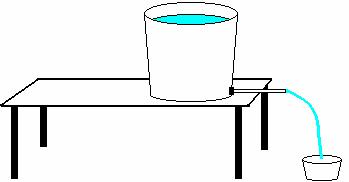
Suppose the 5 gallon bucket were filled to with water to a height, h, and allowed to flow out through the pipe, would the volume flow rate depend on the height, h? Explain your reasoning. Would the volume flow rate depend on the pressure difference between the two ends of the pipe? Explain.
b. If the bucket were filled with water and the water was allowed to flow out through the pipe, but the height of the water in the bucket was kept constant by constantly adding water to the bucket, would the pressure difference between the two ends of the pipe change? Explain.
c. Does the volume flow rate through the pipe depend on the pressure difference between the two ends of the pipe? Explain your reasoning.
d. Determine a method to measure the volume flow rate through the pipe. Explain.
Explain your method to your instructor.
e. Place the stopper end of the pipe into the hole in to the 5 gallon bucket. Test the relationship between the pressure difference between the two ends of the pipe and the volume flow rate by measuring the volume flow rate through the pipe with the water in the bucket kept at a constant height (by constantly adding water to the bucket) at five different heights. Plot your data in an Excel file. Is there a relationship between the volume flow rate and the pressure difference between the two ends of the pipe based on your data? Explain.
The quantitative relationship between volume flow rate and pressure is
![]()
where ![]() †is the pressure
difference across the two ends of the pipe and FV is the volume flow
rate. The constant of proportionality, R, is called the resistance to the flow.
The resistance, R, includes all factors that impede flow.
†is the pressure
difference across the two ends of the pipe and FV is the volume flow
rate. The constant of proportionality, R, is called the resistance to the flow.
The resistance, R, includes all factors that impede flow.
12.2
a. What factors might the resistance to flow depend on? Explain.
b. If the pressure difference between the two ends of the pipe were kept constant by keeping the bucket filled to a height, h, while water was allowed to flow out through the pipe, would the volume flow rate depend on the length of the pipe? Explain.
c. Test your prediction in part b by measuring the volume flow rate for six different lengths of pipe, keeping the pressure at the ends of the pipe constant.
12.3
a. If the pressure difference between the two ends of the pipe were kept constant by keeping the bucket filled to a height, h, while water was allowed to flow out through the pipe, would the volume flow rate depend on the radius of the pipe? Explain.
b. Test your prediction in part a by measuring the volume flow rate for four different diameter pipes, keeping the pressure at the ends of the pipe constant.
12.4
a. In parts 12.1, 12.2, and
12.3 the fluid flowing through the pipe was water. If a different fluid
were used, would you expect the same resistance? Suppose the fluid were
molasses or syrup. Explain.
Poiseuille found that the resistance to flow depends on the length of the pipe, the radius of the pipe, and a measure of the friction within the fluid called viscosity. He found
![]()
where L is the length of the pipe, r is the radius of the pipe and his the viscosity of the liquid.
Since the volume flow rate depends on the resistance and the pressure difference
![]()
with the resistance given by
![]()
one way to measure the viscosity is to measure the flow rate with all other factors (the pressure difference between the two ends of the pipe, the length of the pipe and the radius of the pipe) held constant.
In general, a thicker fluid, like molasses or syrup has a larger viscosity than a thinner fluid, like water.
Equipment:
††††††††††† 1 5 gallon bucket with hole†
††††††††††† 2 1 gallon bucket without holes
††††††††††† various lengths of pipe with various radii with stoppers
1 stopwatch
††††††††††† 1 500 mL graduated cylinder
††††††††††† 1 Excel program
††††††††††† water
††††††††††† 1 waterflow system
13.1
†a. Consider a pipe with a pressure p1 at one end and p2 at the other end, as in the picture below.
![]()
Now consider the same length pipe with the same pressure difference across it, but with a narrower section in the middle, as shown below.†
![]()
Which pipe would have more resistance? Explain.
Which pipe would have the higher flow rate? Explain.
b. Consider again a pipe with a pressure p1 at one end and p2 at the other end, as in the picture below.
![]()
Now consider the following arrangement of pipes, with a pressure difference
p1 - p2 across it.
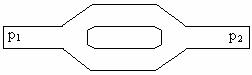
Which would have more resistance, the single pipe, or the arrangement of pipes with two paths? Explain.
Which pipe would have the higher flow rate, the single pipe, or the arrangement of pipes with two paths? Explain.
Test your predictions.
Discuss your reasoning with an instructor.
13.2
a. Consider again the systems of pipes shown in part 3.1.a and 3.1.b. Which system of pipes has a higher resistance (as a system)? Rank the resistance of the three systems. Explain your reasoning. Rank the flow rate of the three systems.
b. Consider the following system of pipes. How would it into your ranking in part a?
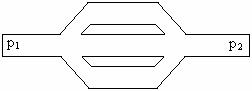
Discuss with an instructor.
Equipment:
††††††††††† 1 waterflow system
14.1 A pump is a means of moving a liquid from a higher pressure to a lower pressure.
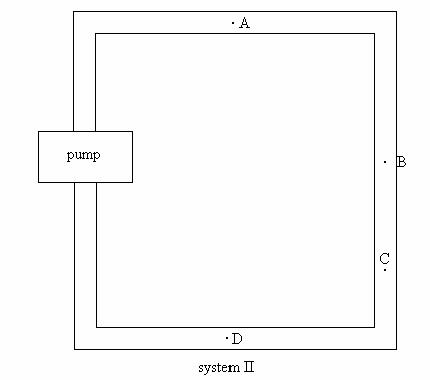
a. Consider the following systems of pumps and pipes. If the pressure difference across the pump were the same in each system, which system would have a higher flow rate at point A? Explain.
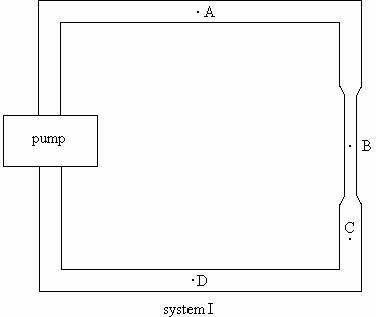
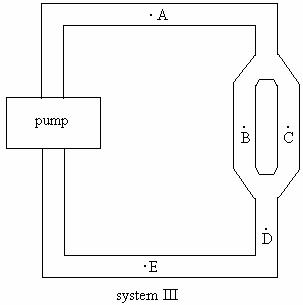
b. Rank the flow rate at points A-E in system III above. Explain. If you cannot rank the flow rates at some of the points explain why you cannot rank them.
c. Rank the pressure at points A-E in system III above. Explain. If you cannot rank the flow rates at some of the points explain why you cannot rank them.
d. Rank the velocity at point A-E. Explain. If you cannot rank the velocity at some of the points explain why you cannot rank them.
e. Obtain the waterflow system III and test your predictions.
14.2
Consider the waterflow system in the diagram below. The cross-sectional area of the narrower pipe is Ĺ the cross-sectional area of the wider pipe.
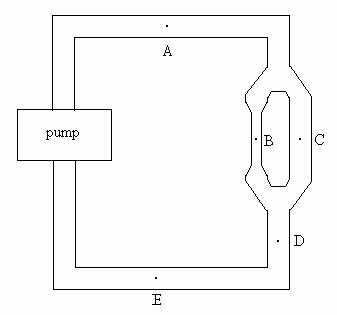
a. Rank the flow rate at points A-E. Explain. If you cannot rank the flow rates at some of the points explain why you cannot rank them.
b. Rank the pressure at points A-E. Explain. If you cannot rank the pressure at some of the points explain why you cannot rank them.
c. Rank the velocity at point A-E. Explain. If you cannot rank the velocity at some of the points explain why you cannot rank them.
d. Obtain the waterflow system and test your predictions.
Equipment:
††††††††††† waterflow system parts
15.1
a. Based on your model of flow in a system with a pump and pipes, construct a model of the circulatory system. Rank the flow rate and pressure in different parts of the system.
b. Set up a similar system of pipes in order to test your model.
Discuss your model to an instructor.
Equipment:
††††††††††† 1 blood pressure measurement kit
16.1 Based on your model for the circulatory system, is your blood pressure the same in all parts of your body? Explain.
†††††††††††
a. Blood pressure is usually measured by an indirect method. Read the handout on measuring blood pressure.
Observe the mercury sphygmomanometer and be able to explain how it works.
Measure the blood pressure of each person in your group.
Equipment:
††††††††††† 1 model of the respiratory system
17.1
a. Obtain the system shown below. Move the membrane in and out, as in the picture and observe what happens to the balloons. Explain the effect in terms of pressure.
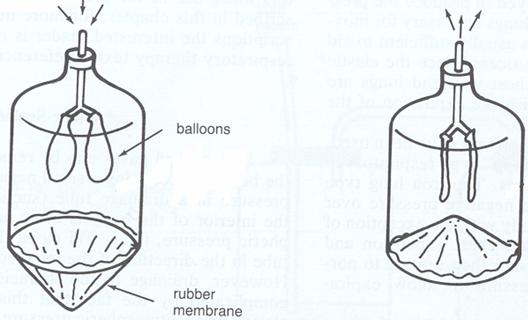
(from
Phyiscs for the Health Sciences 3rd edition by Nave and Nave,
W. B. Saunders Company, Philadelphia, 1985)
b. Explain how this system can be used to model the respiratory system.
SUMMARY
You should understand the concept of pressure. You should understand that for static fluids the pressure at any point in a fluid is the same in all directions and that the pressure at a particular point depends on the depth. You should be able to calculate the pressure at a depth h below the surface of a fluid at rest. You should understand that if the pressure at any point in an enclosed fluid at rest is changed, the pressure is changed by an equal amount at all points in the enclosed fluid (Pascal's Law). You should understand the concepts of volume and density. You should understand that there is a buoyant force on a body immersed in a fluid. You should be able to calculate the buoyant force. You should† understand that whether an object sinks or floats depends on the density of the object and the density of the fluid in which it is immersed. You should understand the concept of mass flow rate. You should understand the concept of volume flow rate. You should† understand the continuity equation both qualitatively and quantitatively. You should understand Bernoulliís Theorem both qualitatively and quantitatively. You should understand how a pump works. You should understand the concept of resistance in dynamic fluid systems. You should understand the relationship between volume flow rate, resistance and pressure in dynamic fluid systems. You should understand the circulatory and respiratory systems in terms of simple models of fluid flow.