UNIT 10

MOMENTUM

 

Objectives

 

 

 

 

 

 

 

 

Equipment:

2 low friction dynamic carts

            1 low friction dynamic track

            Motion Detector

            LoggerPro software

            LabPro computer interface

            2 250g mass bars

 

1.1

 

a. Which of the following objects would be the easiest to stop? Which would be the hardest to stop? Discuss qualitatively how much work it would take to stop each object, the magnitude of the force needed to stop each object, and the amount of time it would take to stop each object. Discuss the properties of the object that determine whether it would be easy or hard to stop.

 

(i) A large, slowly moving truck

 

(ii) A high-speed bullet

 

(iii) A comet moving at a high speed

 

(iv) A slow-pitched softball

 

b. Consider two low friction dynamics carts placed next to each other (The Velcro side of one is next to the magnet side of the other.). Add 500g of mass to one of the carts. Press the trigger on top of one of the carts, releasing a spring, pushing the carts apart. Compare the

 

(i) force exerted on cart one to the force exerted on cart two

 

(ii) time over which the force is exerted on cart one to the time over which the force is exerted on cart two

 

(iii) initial and final velocities (before and after the force is exerted) of cart one and cart two, using a motion detector to measure the final velocity of each cart. You will have to make the measurement twice, measuring the velocity of one cart one time, and the other cart the next time.

 

Calculate the quantity mass times final velocity and the quantity mass times initial velocity for each cart. Compare the quantity for each cart, where m is the mass, vf is the final velocity, and vi is the initial velocity of the cart.

 

c. Two objects are each accelerated by the same constant force for the same time Dt. Using Newton’s Second Law and kinematics, solve for FDt for each object.

 

Show your calculations to an instructor.

 

The quantity mv is called the momentum. We use the symbol p for momentum (); it is measured in units of kgm/s. The quantity FDt is called the impulse. It is sometimes symbolized by I and also has units kgm/s. When a force acts on an object for a time Dt, the change in momentum of the object is given by

 

 

This is called the impulse-momentum theorem. This can also be written

 

 

where

 

or

 

 

Equipment:

1 wooden block

            1 set of “happy/sad” balls

String

            1 balance

            1 rod stand

            1 right angle clamp

            2 rods

            masking tape

           

1.2

 

a. Consider the following situation:

 

You are asleep in your room. You are awakened by the smell of the smoke pouring into your room. The quickest way to close the door is to throw either a blob of clay or a superball laying on your nightstand at the door. There is not time to throw both. Which one would you choose? Explain your reasoning.

 

b. To test your theory in part a Set up the following situation. Obtain a “happy” ball and a “sad” ball (Determine which is which). Stand a wooden block on a table. Hang the “happy” ball (the ball that bounces back when dropped on the floor) from a string from a rod so that when the ball is pulled back, it swings down and hits the block (as in the picture below). The string has to be sufficiently long that the ball will knock the block over. Find the minimum angle the “happy” ball needs to be pulled back, in order to knock over the block. 

 

 

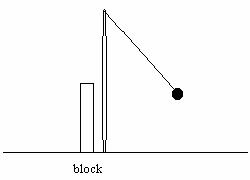
Replace the “happy” ball with the “sad” ball. Release the “sad” ball at exactly the same angle.

 

Discuss qualitatively the relative magnitudes of the force applied to the block in terms of the change in momentum of each block, using the equation above that relates change in momentum to impulse.

           

Equipment:

            Videopoint software

 

2.1

 

a. Open the movie head-on collision in Videopoint. Compare the force exerted, time over which the force is exerted, initial and final velocities (before and after the force is exerted) and the change in momentum of each cart (using the impulse momentum theorem). Assume the mass of a cart is 400g.

 

Show your calculations to an instructor.

 

The law of conservation of momentum states that if the total external force acting on a system is zero (the only forces acting are the forces between the objects in the system), then the final value of the total momentum of the system is equal to the initial value of the total momentum of the system.

 

This can be written mathematically as

 

 

 =

 

 =

 

where  =  is the sum of all of the final momenta of the system and  =  is the sum of all of the initial momenta of the system:

 

The momenta are vector quantities. When working in one dimension, momenta in one direction will be positive and the momenta in the opposite direction will be negative.

 

b. Is this consistent with your results in parts 2.1.a? Explain.

 

Show your results to an instructor.

 

c. Work the following problem:

 

A railroad car of mass 2.50 ´10 4kg is moving with a speed of 4.00 m/s. It collides with three other coupled railroad cars, each of the same mass as the single car, moving in the opposite direction with an initial speed of 2.00 m/s. After the collision the single railroad car has a final speed of 5 m/s opposite to its original direction. What is the final speed of the three-coupled car after the collision?

 

Show your work to an instructor.

 

Equipment:

2 low friction dynamic carts

            1 low friction dynamic track

            Motion Detector

            LoggerPro software

            LabPro computer interface

           

2.2

 

a. Collide two low friction dynamics carts so that they stick together. Measure the initial velocity of each cart and the final velocity of the two carts stuck together with the motion detector. Calculate the total kinetic energy of the two carts before the collision and the total kinetic energy after the collision. How does the total kinetic energy before the collision compare to the total kinetic energy after the collision?

 

b. Calculate the total kinetic energy before the collision and the total kinetic energy after the collision for the gliders in part 2.1.a. How does the total kinetic energy before the collision compare to the total kinetic energy after the collision?

 

A collision is considered to be elastic if the total initial kinetic energy is equal to the total final kinetic energy. We say that the kinetic energy is conserved. A collision is considered to be inelastic if the total initial kinetic energy is not equal to the total final kinetic energy. We say that the kinetic energy is not conserved in an inelastic collision.

 

c. Were the collisions in parts 2.1.a and 2.2.a elastic or inelastic? Explain. 

 

When two objects stick together, the collision is completely inelastic and kinetic energy is not conserved. When objects bounce apart, kinetic energy may or may not be conserved.

 

Equipment:

            4 large mass hangers

            1 mass set (large)

            1 rod

            1 meterstick

            1 chain

            1 finely calibrated measuring device

            1 piece of wood

            1 scale

 

3.1 We are going to put together all that we have learned about work, energy and momentum to determine whether or not your hand has enough kinetic energy to break a piece of wood (as done by martial artists). 

 

a. First we are going to calculate the amount of work needed to break a board by hanging mass from the board (applying a force) and measuring the displacement of the center of the board (distance).

 

Rest a piece of wood between two tables. Put a rod across the top of the center of the wood and hang a chain from one side of the rod to the other (below the wood). Hang four large mass hangers from the chain. Place a finely calibrated ruler so that you can read the distance the center of the board moves each time you add mass.  

 

You are going to add mass to the mass hangers, about 5-6kg at a time at first. Record the distance the center of the board moves and the amount of mass added each time. When the board is close to breaking, add smaller amounts of mass each time.

 

In order to calculate the amount of work done in breaking the board, you will have to calculate the amount of work done each time you added mass and then sum all the work done to get the total work.

 

Calculate the total work done in breaking the board.

 

If all of the kinetic energy of your hand went into breaking the board, what would be the velocity of your hand needed to break the board?

 

Not all of the kinetic energy of your hand will go into breaking the board. In order to estimate the amount of kinetic energy of your hand that goes into breaking the board, we are going to assume that the collision between your hand and the board is inelastic.

 

b. We are going to use conservation of momentum to find the final velocity of your hand after breaking the board.

 

You will need to

 

(i) measure the velocity your hand would be moving, if you were to break the board. Use a motion detector to measure the velocity of your hand.

 

(ii) estimate the mass of your hand.

 

(iii) measure the mass of a board.

 

Use conservation of momentum for an inelastic collision to find the velocity of your hand after breaking the board.

 

c. Determine the change in kinetic energy of your hand in order to determine the amount of kinetic energy that goes into breaking the board. Based on your calculation, would you like to attempt to break the board? Explain.

 

d. OPTIONAL ACTIVITY –

 

After signing the release form (Sheet 1), attempt to break a board.

 

SUMMARY

 

At the end of this unit you should understand the concept of momentum, the concept of impulse, the relationship between impulse and change in momentum and be able to work problems using the impulse-momentum theorem. You should understand and be able to work problems using the concept of conservation of momentum. You should understand that kinetic energy is not always conserved in a collision. You should be able to use your knowledge of work, kinetic energy, conservation of energy and momentum to work problems.

Sheet 1

 

After duly considering the situation, I have convinced myself and my instructor that I can break a board, and I want to try it. I understand that the activity is optional. The instructors and Physics Department are not responsible for any injury that may result.

 

 

 

Your signature                                                                               Date                      

 

Instructor's  signature                                                                    Date