UNIT 9

ENERGY

Objectives

• To understand the concept of kinetic energy

• To understand the relationship of net work to the change in kinetic energy

• To understand the concept of a conservative force

• To understand that the work done by a conservative force can be defined as a change in potential energy

• To understand that the gravitational force is a conservative force and that the work done by the gravitational force can be expressed as a change in potential energy

• To understand the concept of gravitational potential energy

• To understand the relationship of work done by other forces (besides the gravitational force) to the change in kinetic energy and gravitational potential energy of an object

• To be able to work problems involving work, change in kinetic energy and change in gravitational potential energy

Equipment:

1 Fan cart

You may need:

1 force sensor

1 mass set

1 mass hanger

string

Motion Detector

LoggerPro software

LabPro computer interface

1 low friction dynamics track

1 spring scale

1.1

a. Devise a method for measuring the force of air on a fan cart. Describe your method.

b. Carry out your method and measure the force of air on a fan cart.

Discuss your method with an instructor.

c. Does the force of the air on the fan cart change if you add mass to the fan cart? Explain your reasoning.

Discuss your method with an instructor.

d. Calculate the work done by the air on a fan cart with a 200g mass attached to it traveling at least 1m. Show your work.

e. Calculate the work done by the air on a fan cart with a 500g mass attached to it traveling the same distance. Show your work.

Equipment:

1 Fan cart

Motion Detector

LoggerPro software

LabPro computer interface

200g mass

500g mass

masking tape

1 meterstick

1.2

a. If the work done by friction is practically zero, what is the net work done on each of the fan carts in parts 1.1.c and 1.1.d List properties of the fan carts that change or remain the same before, during and after the work is done.

b. Use a motion detector to determine the final velocity of each cart in parts 1.1.c and 1.1.d What is the initial velocity of each cart?

c. Calculate the quantity ½ mv_f² for each cart, v_f is the final velocity.

The quantity ½ mv² is called kinetic energy. The symbol for kinetic energy is K or KE. Energy is measured in Joules (J). ½ mv_f² is the final kinetic energy, KE_f. ½ mv_i² is the initial kinetic energy, KE_i.

d. Compare the change in kinetic energy (the final kinetic energy minus the initial kinetic energy) of each cart.

It can be shown theoretically (using calculus) and has been verified experimentally that the work done on an object is equal to the change in kinetic energy of the object.

Mathematically,

W_net = ½ mv_f² - ½ mv_i²

which can be written

W_net = KE_f - KE_i = DKE

e. Is this consistent with your data in parts a. and c. above?

Equipment:

None

2.1

a. A block is to be lowered from point a to point b, a distance of 20m vertically, as in the diagram below.

Calculate the work done by the gravitational force in each of the cases below:

(i) The block is dropped vertically 20m.

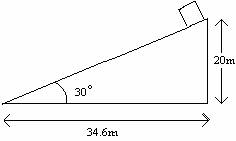
(ii) The block is placed at the top of an inclined plane at an angle of 30° to the horizontal (as in the picture below), slid down the plane and then pushed 34.6m to point b.

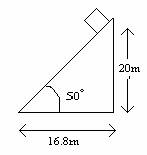
(iii) The block is placed at the top of an inclined plane at an angle of 50° to the horizontal (as in the picture below), slid down the plane and then pushed 16.8m to point b.

b. Based on your calculations in part a, does the work done by the gravitational force in moving an object from point a to point b depend on the path taken by the object in moving from point a to point b?

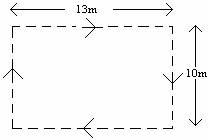
c. The same block is moved in a vertical loop: up 10m, across 13m, down 10m and back across 13m, as in the diagram below. What is the total work done by the gravitational force in moving the block around the loop? Show your work.

d. What was the total work done by the gravitational force in moving a block around a loop in Unit 8 1.3.e?

e. Based on the results of parts c and d, what is the total work done by the gravitational force when an object moves through a closed loop (ends at the same point that it starts)? Explain.

A force is called a conservative force if it has the following properties:

1) The work done by the force on a particle moving between any two points is independent of the path taken by the particle.

2) The work done by the force on a particle moving through any closed path (a path in which the beginning and end points are identical) is zero.

f. Based on your experiments in parts a through e above, is the gravitational force a conservative force?

All experimental evidence indicates that the gravitational force is a conservative force.

If a force is a conservative force, the work done by the force depends only on the end points (the beginning and starting points). Near the surface of the Earth, the gravitational force is downwards (vertical), and the work done when moving an object horizontally (parallel to the Earth’s surface) is zero. The work done by the gravitational force can be written as

W_g = -(mgy_f – mgy_i)

Where y_f is the final height of the object, y_i is the initial height of the object, g = 9.8m/s² and m is the mass of the object. The quantity mgy is called the gravitational potential energy of the object. mgy_f is the final gravitational potential energy of the object and mgy_i is the initial gravitational potential energy of the object. We will use the symbol PE for gravitational potential energy. Technically, we should write a subscript PE_g, or indicate in some manner that it is the gravitational potential energy, since there are other kinds of potential energy, but at this point, we will just use the symbol PE. (The symbol U is also used sometimes for potential energy.) Gravitational potential energy is measured in Joules (J). The work done by the gravitational force can then be written

W_g = -(PE_f – PE_i) = -DPE

Equipment:

1 Daredevil Speedway

2.2

a. Obtain a Daredevil Speedway set up with a single loop. If the car is not “wound”, so that no other force is acting on the car to move it forward besides the initial force of the launcher, and friction is considered to be negligible,

(i) what must be the minimum velocity of the car at the top of the loop in order for the car to remain in contact with the loop at the top and not fall off the track. You may wish to refer to Unit 7 1.4.d in order to determine the velocity. Show your work.

(ii) what must be the minimum kinetic energy of the car at the top of the loop? Show your work.

(iii) what must be the minimum kinetic energy with which the car leaves the launcher? Show your work.

Show your calculations to an instructor.

When the gravitational force is the only force acting on an object, the net work on the object is the total work done by the gravitational force. This can be expressed mathematically as follows:

W_net = W_g

W_g = -DPE

W_net = -DPE = DKE

-(PE_f – PE_i) = KE_f -KE_i

or PE_i + KE_i = PE_f + KE_f

mgy_i +1/2mv_i² = mgy_f +1/2mv_f²

This is called the conservation of energy, since the initial energy is equal to the final energy. This equation is only true if the gravitational force is the only force acting on the object.

b. Test to see if the car leaves the launcher with the minimum kinetic energy necessary to maintain contact with the loop and not fall off the track.

Equipment:

Videopoint software

Daredevil speedway video

2.3

a. Consider a Daredevil Speedway with a number of loops and a ramp. A car can be “wound” a number of times and started with the launcher. If the car is “wound”, there is a force pushing the car forward, while it is in motion. Consider a “wound” car started with a launcher. If friction is negligible, write an equation for the work done by the force pushing the car forward after it leaves the launcher, relating it to the work done by the gravitational force and the kinetic energy.

Show your equation to an instructor.

b. Is the work done by the force pushing the car forward a conservative force? Explain your reasoning.

When work is done on an object both by the gravitational force and other forces, the net work is the sum of the work done by the gravitational force and the work done by other forces. The work done by other forces is the sum of the change in the gravitational potential energy and the change in the kinetic energy of the object. This can be seen mathematically as follows:

W_net = W_other + W_g = DKE

W_other = -W_g + DKE

W_other = DPE + DKE

W_other = (PE_f – PE_i) + (KE_f – KE_i)

W_other = (PE_f + KE_f) – (PE_i + KE_i)

W_other = (mgy_f + 1/2mv_f²) – (mgy_i + 1/2mv_i²)

c. Use the Videopoint software to view a Daredevil Speedway video. Determine the initial velocity of the car after it leaves the launcher and the final velocity of the car at the end of the track. Calculate the work done by the force pushing the car forward.

SUMMARY

At the end of this unit you should understand the concept of kinetic energy and the relationship of net work to the change in kinetic energy. You should understand the concept of a conservative force and be able to distinguish a conservative force from a non-conservative force. You should understand that the gravitational force is a conservative force and that the work done by the gravitational force can be expressed as a change in potential energy. You should understand the relationship of work done by other forces (besides the gravitational force) to the change in kinetic energy and gravitational potential energy of an object. You should be able to work problems involving work, change in kinetic energy and change in gravitational potential energy.