UNIT 6
STATICS AND TORQUE
Objectives
- to understand the concept of torque
- to be able to calculate torques
- to understand the concept of static equilibrium
- to be able to solve problems involving static equilibrium
1.1 Set up a rotary motion sensor with a rod attached to the middle, as in the picture below (Use a rod stand to support the rotary motion sensor).
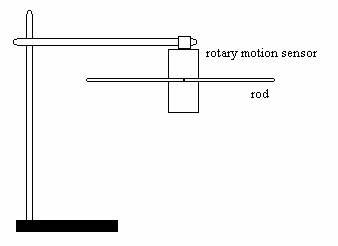
a. Add equal masses to each side of the rod so that the rod does not rotate, but is balanced (parallel to the table). Draw or explain the arrangement of masses that balances the rod. Is there more than one arrangement that will balance the rod? Explain why the rod is balanced.
b. Add an additional mass to one side of the rod. Again arrange the masses so that the rod is balanced (parallel to the table). Draw or explain the arrangement of masses that balances the rod. Is there more than one arrangement that will balance the rod? Explain why the rod is balanced.
c. Consider a rod that is free to rotate, as in the picture below. If the following arrangement of masses were placed on the rod while someone was holding it level, then the rod was released, would the rod remain balanced? Explain.
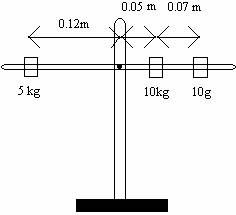
d. Draw a force diagram for the situation in part c. Determine the total force upwards and the total force downwards. Does the force diagram explain why the rod does or does not remain balanced?
e. In the situation in part d, does it matter (for determining whether the rod is balanced) where the force is exerted on the rod? Explain.
1.2
a. Calculate the quantity force times the distance from the fulcrum for each mass for the situation in part 1.1.c. Compare the sum of this quantity for each mass on the left side to the sum of this quantity for each mass on the right side.
b. Consider the diagram below. If the following arrangement of masses were placed on the rod while someone was holding it level, then the rod was released, would the rod remain balanced? Explain.
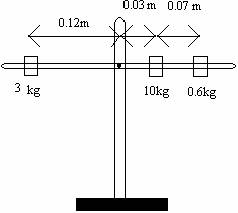
c. Calculate the quantity force times the distance from the fulcrum for each mass for the situation in part b. Compare the sum of this quantity for each mass on the left side to the sum of this quantity for each mass on the right side.
We will call r the distance between the pivot point
and the point of application of the force F. Actually, it is only the
component of the force that is perpendicular to a line through the pivot point
and the point of application of the force that does the turning. This will be
explained in more detail in Unit 6 Reading A. We will call the component
of the force that is perpendicular to a line through the pivot point and the
point of application,![]() . The quantity r times
. The quantity r times ![]() , is called the torque, t. Torque is measured in units Nm. In equation
form
, is called the torque, t. Torque is measured in units Nm. In equation
form
t = r ![]()
1.3
a. Calculate the torque for each mass on each side of the rod for the situation in 1.1.c. Compare the sum of the torques on the left side of the rod to the sum of the torques on the right side of the rod.
b. Calculate the torque for each mass on each side of the rod for the situation in 1.2.b. Compare the sum of the torques on the left side of the rod to the sum of the torques on the right side of the rod.
c. Based on your calculations in parts a and b, does a calculation of the sum of the torques on each side of the rod determine whether or not a rod will balance? Explain.
Each applied force will tend to rotate the object clockwise or counterclockwise. We can think of the resulting torque due to that force as being clockwise or counterclockwise. It is convenient to label one direction of torque positive and the other direction of torque negative.
The sum of all the torques on the balance is the net torque.
d. What is the net torque on the rod in parts a and b above?
When an object is not rotating, the net torque on the object is zero. If the net torque on an object is not zero, the object will rotate.
Mathematically, the net torque is written as
![]()
![]()
where a torque is positive if it causes a clockwise rotation and negative if it causes a counterclockwise rotation.
2.1 If the net torque on an object equals zero, the object will not rotate. If the net force on an object equals zero, then the object will not move. If both the net force and the net torque are zero, then the object is said to be in static equilibrium.
When working problems involving torque and forces, it is useful to draw the force diagram with the forces drawn at the point they are exerted. For example, the situation in part 1.2.b, the force diagram would be drawn like this:
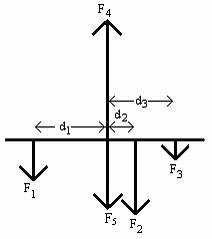
where F1 is force of the 3kg mass on the rod, F2 is the force of the 10kg mass on the rod, F3 is the force of the 0.6kg mass on the rod, F4 is the upward force of the pivot on the rod and F5 is the mass of the rod. d1, d2 and d3 are the distances of the masses from the pivot. Forces F4 and F5 are at the pivot.
If the rod is not moving, the net force on the rod is zero and this can be written mathematically as
F1 + F2 + F3 + F4 + F5 = 0
If the rod is not rotating, the net torque on the rod is zero. You may choose to calculate the torque about any point on the object. In some cases, like this one, it is natural to take the torque about the pivot point. In this case the torque due to forces F4 and F5 are zero, because the distance between the force and the pivot point is zero. This can be written mathematically as
t1 + t2 + t3 = 0
or
F1 d1 – F2 d2 – F3 d3 = 0
The point about which you take the torque may depend on the problem and which quantities are known and unknown.
Here is an example problem:
In the diagram below a pole vaulter carries a 6.0m long pole by pushing down with his right hand and up with his left hand. The pole is uniform and has a mass on 10kg. Find the forces FR and FL. The weight of the pole is considered to act at the center of the pole. This is explained in Unit 6 Reading A.
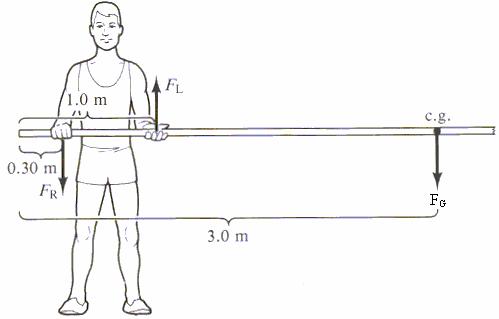
(from Physics with Health Science Applications by Paul Peter Urone, John Wiley and Sons, NY, 1986)
(1) Focus on the Problem: What’s going on?
The pole vaulter is holding the pole so it does not rotate and it does not move – the pole is in equilibrium. The net torque and the net force on the pole are zero.
We want to find the upward force due to his left hand and the downward force due to his right hand.
(2) Describe the Physics: What is the physics?
Draw a force diagram.
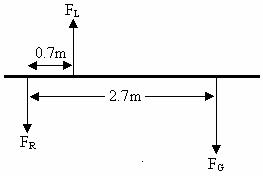
It does not matter where we choose the pivot. We will arbitrarily choose the pivot to be at the position of his right hand.
The known distances from the pivot are
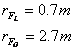
The gravitational force on the pole is known
![]()
Write down the equations for the net force and the net torque.

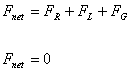
(3) Plan the Solution: Can we find the solution?
Use the fact that the net torque and the net force are zero to solve for FL and FR.
(4) Execute the Plan: What is the answer?
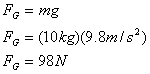

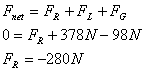
The upward force of the left hand is 378N and the downward force of the right hand is 280N.
(5) Evaluate the Answer: Can this be true?
This is a reasonable answer because the larger force is at a shorter distance from the pivot point.
a. Work the following problem:
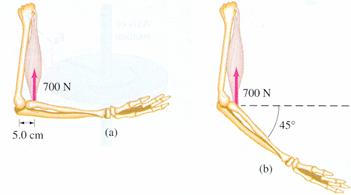
Consider an arm at rest, as in each of the two pictures below. The biceps muscle exerts a vertical force upward on the lower arm as shown in the diagrams below. There is also a force, not shown, exerted downward at the elbow joint.
(from Physics Forth
Edition, Douglas C. Giancoli, Prentice hall, New
i) For diagram (a) calculate the torque about the axis of rotation through the elbow joint due to the weight of the lower arm and hand. Assume the muscle is attached 5.0cm from the elbow. Show your work.
ii) For diagram (b) calculate the torque about the axis of rotation through the elbow joint due to the weight of the lower arm and hand. Assume the muscle is attached 5.0cm from the elbow. Show your work.
SUMMARY
You should understand the concept of torque and be able to
calculate torques. You should understand the concept of static equilibrium and
be able to solve problems involving static equilibrium.