UNIT 3

GRAVITATIONAL FORCE AND TWO-DIMENSIONAL MOTION

Objectives

· To use Newton’s Laws to understand the nature of the gravitational force.

· To understand the acceleration of objects near the surface of the Earth due to the gravitational force.

· To understand the difference between the gravitational force and the mass.

· To understand position, velocity, and acceleration as vector quantities and use them to describe motion in two-dimensions.

• To understand that motion in two-dimensions can be separated into x- and y-components which can be treated independently.

• To be able to use kinematics equations to describe the motion of objects in two-dimensions.

Watch the following video clip from Doane College.

Equipment:

Motion Detector

LoggerPro software

LabPro computer interface

Super ball

Softball

2 kg mass

Bathroom scale

Balance

Standard masses

1.1 In Unit 1 you observed that falling objects accelerate at the same rate near the surface of the Earth when there is very little friction.

a. Consider a super ball dropped from 2.5 meters above the floor and allowed to bounce three or four times. Draw the position vs. time, velocity vs. time, and acceleration vs. time graphs for the whole motion of the ball, including the bounces. Explain why you drew the graphs the way you did.

b. Set up the Motion Detector and take data for the situation in part a.

c. Discuss the velocity and acceleration of the ball at three different points:

(i) the ball is rising after the bounce.

(ii) the ball at its maximum height after the bounce.

(iii) the ball falling.

d. Discuss whether the velocity and the acceleration are positive, negative, or zero in each of the three cases in part c.

e. Suppose the Motion Detector had been on the floor, instead of above the ball, would your answers in part c and part d change?

Discuss your answers with an instructor.

1.2

a. If an object is undergoing constant acceleration near the surface of the Earth, then, based on observations in Unit 2, it must be experiencing a force. This force is called the gravitational force. Calculate the magnitude of the gravitational force on the ball you used in part 1.1.

Explain to an instructor how you calculated the magnitude of the force.

b. Do all objects accelerating near the surface of the Earth experience the same gravitational force? Explain.

c. Calculate the gravitational force of three objects:

(i) softball.

(ii) 2kg mass.

(iii) you.

d. Would the objects in part c. experience the same acceleration if dropped from a high building? Explain.

e. Is there a difference between the mass of the object and the gravitational force on an object? Explain.

The gravitational force on an object is called its weight.

f. Discuss with your partners the concepts of mass, gravitational force, weight, and gravitational acceleration near the surface of the Earth.

Equipment:

VideoPoint software

Excel Program

2.1 Until now we have been observing objects moving in one dimension.

a. Watch the following movie.

b. Is the object accelerating in the y-direction? Explain.

c. Is there a force on the object in the y-direction? Explain.

d. Is the object accelerating in the x-direction? Explain.

e. Is there a force on the object in the x-direction? Explain.

f. Draw the position vs. time, velocity vs. time, and acceleration vs. time graphs for the motion of the ball in each direction (draw each of the three graphs for the x-direction and each of the three graphs for the y-direction), after it was released by the girl.

g. Open the VideoPoint software. First, choose Open Movie. Choose the movie projectile A in a folder named movies & files, located in your group folder. On the window Number of Points, enter 1 and click on OK. Advance the film frame by frame, to frame 6, until her hand releases the ball. Click on the ball in the picture. This will record the x- and y-position of the ball and advance the movie one frame. Continue clicking on the ball in each frame, until the end of the movie. Click on the Graph icon on the left toolbar. Select y under Vertical axis. Click on Position, Velocity, and Acceleration. Click on OK. Is the data consistent with your predictions in part f?

h. Select graph again and this time select x under vertical axis. Click on Position, Velocity and Acceleration. Click on OK. Change the limits on the vertical axis to –1000 and 1000 on the velocity graph and –10000 and 10000 on the acceleration graph by clicking on the lower and upper limits of the graph. Is the data consistent with your predictions in part f?

The equations of motion can be applied independently to the x- and y- directions.

Where v_xi is the initial velocity in the x-direction, v_xf is the final velocity in the x-direction, v_yi is the initial velocity in the y-direction, v_yf is the final velocity in the y-direction, a_xi is the initial acceleration in the x-direction, a_xf is the final acceleration in the x-direction, a_yi is the initial acceleration in the y-direction, and a_yf is the final acceleration in the y-direction.

2.2

a. Two identical balls are released from the same height at the same time. The first ball is simply dropped. The second ball has an initial velocity, v, parallel to the ground. Which ball will hit the ground first?

b. Two balls, one of mass m and one of mass 4/3m, are released in the same manner as in problem a above. Which ball will hit the ground first? Explain your reasoning.

c. Watch the following videoclip. Is this consistent with your answer to part a.? Explain.

2.3 Work the following problem:

Consider an athlete jumping a hurdle as in the picture below.

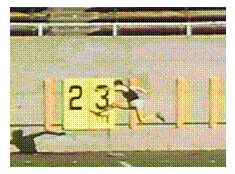
a) Using words (position, velocity, and acceleration etc.), describe in detail the motion of a point on the runner's body, focus on a point on the runner’s upper body, as he leaves the ground, goes over the hurdle, and lands on the ground.

b) If you focus on a point on the runner’s upper body, how does motion while the runner is in the air compare to the motion of a ball in the air? Explain.

c) The hurdle is 1.0m high and the runner’s initial speed leaving the ground is 8m/s. The

distance he jumps is 2.5m. Calculate the angle at which he leaves the ground. Show your

work.

d) How long is he in the air? Explain your reasoning

e) Does he clear the hurdle? Explain your reasoning.

Summary

You should be able to use Newton’s Laws to understand the nature of the gravitational force. You should know the difference between the gravitational force and the mass. You should understand position, velocity, and acceleration as vector quantities and be able to use them to describe motion in two-dimensions. You should understand that motion in two-dimensions can be separated into x- and y-components. To be able to use kinematics equations to solve problems about motion in two-dimensions.