UNIT 15 EXERCISES

1) The angular speed of a point 1.2m from the center of a steadily rotating merry-go-round rotates one complete revolution in 4.0 seconds.

a) What is the angular speed of the point? Show your work.

b) What is the linear speed of the point? Show your work.

c) What would be the angular acceleration of a child placed at this point? Show your work.

2) A centrifuge rotor, similar to the one seen in unit 7, is accelerated from rest to 20,000 revolutions per minute (rpm) in 5.0min.

a) What is its average angular acceleration?

b) Through how many turns has the centrifuge rotor turned during its acceleration period? Assume constant angular acceleration.

3) How fast (in rpm) must a centrifuge rotate if a particle 7.5cm from the axis of rotation is to experience an acceleration of 100,000g’s. Where one g = 9.8m/s².

4) At a particular moment in a race, a car roaring around a turn, pictured below, with a radius of 50m had an angular speed of 0.60rad/s and an angular acceleration of 0.20rad/s².

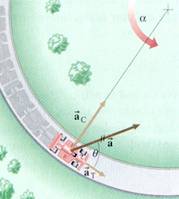
At this particular moment find

a) the linear speed. Show your work.

b) the centripetal acceleration. Show your work.

c) its total linear acceleration. Show your work.