UNIT 7 EXERCISES

1) You and your niece are sitting in an airplane. You have a window seat. The airplane makes a level turn of radius 2.0km at a speed of 400km/hr. The coefficient of static friction between the airplane seat and a person is 0.35.

a) Suppose there were no friction. Draw a force diagram for you or your niece for the case of no friction. Describe your motion if there were no friction.

b) Now assume there is friction. Draw a force diagram for you or your niece for this case.

c) Is the frictional force sufficient to keep you moving in a radius of 1.0km at a speed of 400km/hr? Would you slide in your seat? Show your work.

2) Consider a car rounding a curve with radius r at a constant speed as pictured below.

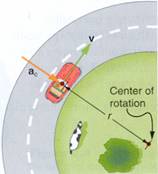
(from College Physics by Paul Peter Urone, Brooks/Cole Publishing Company, NY, 1998)

a) Calculate the frictional force needed for a 900kg car traveling around a 500m radius curve at 25.0m/s, if the car is to continue moving in a circle and not slide. Assume an unbanked curve. Show your work and explain your reasoning.

b) If the road is wet and the coefficient of static friction is 0.19, at what velocity would the car begin to slide into the other lane? Show your work and explain your reasoning.

c) If the curved were banked at 13^o, and there were no friction, at what velocity would the car begin to slide into the other lane? Show your work and explain your reasoning.

3) A ball of mass 150 grams on the end of a 1.10m long massless cord is swung vertically as in the picture below.

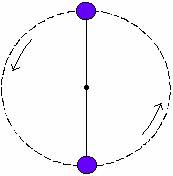
a) Determine the minimum speed the ball must have at the maximum height of its motion so that it continues moving in a circle. Show your work.

b) Determine the force of the cord on the ball at the minimum height of its motion if the ball is moving at twice the speed found in part a. Show your work.

4) Calculate the velocity of a satellite moving in a circular orbit about Earth at a height of 3600km above the surface of Earth.